题目内容
10. 如图是质谱仪工作原理的示意图.带电粒子a、b经电压U加速(在A点初速度为零)后,进入磁感应强度为B的匀强磁场做匀速圆周运动,最后分别打在感光板S上的x1、x2处.图中半圆形的虚线分别表示带电粒子a、b所通过的路径,则( )
如图是质谱仪工作原理的示意图.带电粒子a、b经电压U加速(在A点初速度为零)后,进入磁感应强度为B的匀强磁场做匀速圆周运动,最后分别打在感光板S上的x1、x2处.图中半圆形的虚线分别表示带电粒子a、b所通过的路径,则( )| A. | a的质量一定大于b的质量 | B. | a的电荷量一定大于b的电荷量 | ||
| C. | a运动的时间小于b运动的时间 | D. | a的比荷($\frac{{q}_{a}}{{m}_{a}}$)小于b的比荷($\frac{{q}_{b}}{{m}_{b}}$) |
分析 带电粒子先在匀强电场中做匀加速直线运动,再进入磁场做匀速圆周运动,轨迹为半圆,本题动能定理和牛顿第二定律求解.
解答 解:设粒子经电场加速后的速度大小为v,磁场中圆周运动的半径为r,电荷量和质量分别为q、m,打在感光板上的距离为S.
根据动能定理,得
qU=$\frac{1}{2}$mv2
解得:v=$\sqrt{\frac{2qU}{m}}$
由qvB=m$\frac{{v}^{2}}{r}$
解得:r=$\frac{mv}{qB}$=$\frac{1}{B}\sqrt{\frac{2mU}{q}}$
则S=2r
得到:$\frac{q}{m}$=$\frac{8U}{B{S}^{2}}$
由图,Sa<Sb,U、B相同,则$\frac{{q}_{a}}{{m}_{a}}$>$\frac{{q}_{b}}{{m}_{b}}$;
而周期T=$\frac{2πm}{Bq}$,因此它们的运动时间是周期的一半,
由于$\frac{{q}_{a}}{{m}_{a}}$>$\frac{{q}_{b}}{{m}_{b}}$,所以a运动的时间小于b运动的时间,故C正确,ABD错误;
故选:C.
点评 本题属于带电粒子在组合场中运动问题,电场中往往用动能求速度,磁场中圆周运动处理的基本方法是画轨迹.

练习册系列答案
相关题目
1.如图所示,是演示自感现象的实验电路图.下列说法中正确的是( )


| A. | 在断开开关S后的一段短暂时间里,A中仍有电流通过,方向为a→b | |
| B. | 在断开开关S后的一段短暂时间里,L中仍有电流通过,方向为a→b | |
| C. | 在断开开关S后,原存储在线圈内的大部分磁场能将转化为电能 | |
| D. | 在断开开关S后,原存储在线圈内的大部分磁场能将转化为化学能 |
19.能正确表示简谐运动的回复力与位移关系的图象是图中的( )
| A. |  | B. |  | C. |  | D. |  |
 如图所示,置于圆形水平转台边缘的小物块随转台加速转动,当转速达到某一数值时,物块滑离转台开始做平抛运动.现测得转台半径R=0.5m离水平地面的高度H=0.8m,物块与转台间的动摩擦因数为μ=0.2,设物体所受的最大静摩擦力等于滑动摩擦力,重力加速度取10m/s2求:
如图所示,置于圆形水平转台边缘的小物块随转台加速转动,当转速达到某一数值时,物块滑离转台开始做平抛运动.现测得转台半径R=0.5m离水平地面的高度H=0.8m,物块与转台间的动摩擦因数为μ=0.2,设物体所受的最大静摩擦力等于滑动摩擦力,重力加速度取10m/s2求:

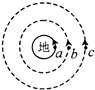 如图,a是静止在地球赤道上的物体,b、c是两颗人造地球卫星,其中c是地球的同步卫星,a、b、c在同一平面内沿不同的轨道绕地心做匀速圆周运动,三者绕行方向相同(为图示逆时针方向),已知Rb<Rc.若在某一时刻,它们正好运行到同一条直线上,如图甲所示.那么再经过6小时,物体a、卫星b、c的位置可能是下图中的( )
如图,a是静止在地球赤道上的物体,b、c是两颗人造地球卫星,其中c是地球的同步卫星,a、b、c在同一平面内沿不同的轨道绕地心做匀速圆周运动,三者绕行方向相同(为图示逆时针方向),已知Rb<Rc.若在某一时刻,它们正好运行到同一条直线上,如图甲所示.那么再经过6小时,物体a、卫星b、c的位置可能是下图中的( )


