题目内容
【题目】如图所示,在高度均为L的条形区域Ⅰ、Ⅱ中分别存在匀强磁场和匀强电场,区域Ⅰ内的磁场方向垂直于纸面向里,区域Ⅱ内的电场方向竖直向上、电场强度大小为E.M、N是涂有荧光物质的水平板,其中M板位于匀强磁场的上边界,N板位背匀强电场的下边界.观有一束电子从O点(在磁场内部,且紧贴M板)连续不断地水平向右射入磁场,电子束由两部分组成,一部分为速度大小为v的低速电子,另一部分为速度大小为2v的高速电子,当Ⅰ区中磁场较强时,M板出现两个亮斑,缓慢改变磁场的强弱,直至M板上的亮斑恰好消失为止,此时可观察到N板有两个亮斑.已知电子质量为m、电荷量为e,电子间的相互作用不计,磁场下边界上没有磁场,但有电场,不计电子重力.求:
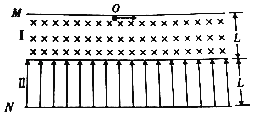
(1)N板出现两个亮斑时Ⅰ区内磁场的磁感强度大小B;
(2)到达N板左方亮斑的电子在磁场和电场中运动的时间t;
(3)N板两个亮斑之间的距离x.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据题意作出电子运动轨迹,求出电子轨道半径,洛伦兹力提供向心力,由牛顿第二定律求出磁感应强度.
(2)求出电子在磁场与电场中的运动时间,然后求出电子总的运动时间.
(3)求出两电子到达N板的位置,然后求出两亮斑间的距离.
(1)低速电子速度恰好与两场交界相切且速度方向与电场垂直时M板上的亮斑消失,此时两电子运动轨迹如图所示: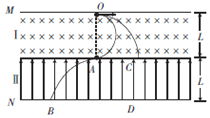
低速电子轨道半径:r1=![]() ,高速电子轨道半径:r2=L,
,高速电子轨道半径:r2=L,
电子在磁场中做圆周运动,洛伦兹力提供向心力,
由牛顿第二定律得:evB=m![]() ,解得:
,解得:![]() ;
;
(2)低速电子打在N板的左侧,该电子在磁场中的运动时间为半个周期,
在磁场中的运动时间:![]() ,
,
低速电子在电场中做类平抛运动,![]() ,解得:
,解得:![]() ,
,
到达N板左方亮斑的电子在磁场和电场中运动的时间:t=t1+t2=![]() ;
;
(3)高速电子沿电场线方向进入电场,到达N板时与O带你的水平距离:x1=L,
低速电子在电场中做类平抛运动,沿板方向运动的距离:x2=vt2=v![]() ,
,
N板两亮斑间的距离:x=x1+x2=L+v![]() ;
;

 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案