��Ŀ����
����Ŀ����ͼ��ʾ������M=10kg���ϱ���⻬���㹻����ľ����F=50N��ˮƽ���������£��Գ��ٶ�v0=5m/s��ˮƽ�������������˶��������㹻����ͬ��С���飨����Ϊ�ʵ㣩�����ǵ�����Ϊm=1.0kg����һ��С�������ٵط����������˶�ľ������Ҷˣ���ľ���˶���L=1.0mʱ�������ٶȵ���ľ������Ҷ˷��ϵ�2��С���飬����ظ���ֻҪľ���˶���L����ľ������Ҷ����ٶȷ���һ��С���飮ȡg=10m/s2 �� ��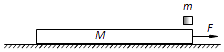
��1��ľ��������Ķ�Ħ��������
��2����1��С������Ϻ�ľ����ٶȴ�С��
��3����1��С������Ϻ�ľ���˶���Lʱ��ľ����ٶȴ�С��������С����Ϻ�ľ���˶��˶���Lʱģ����ٶȣ�
���𰸡�
��1���⣺��ľ��������Ķ�Ħ������Ϊ�̣���ľ���ص��������˶��������У�F=��Mg
����= ![]() =
= ![]() =0.50
=0.50
��ľ��������Ķ�Ħ������Ϊ0.5
��2���⣺��l��С������ŵ�ľ���ϣ�ľ�����ȼ����˶�������ϵ�l��С���飬ľ�����ȼ����˶��ļ��ٶȴ�СΪa1������ţ�ٵڶ������У�
�̣�M+m��g��F=Ma1
��ã�a1= ![]() =0.50m/s2
=0.50m/s2
�𣺵�1��С������Ϻ�ľ����ٶȴ�СΪ0.50m/s2
��3���⣺�����˶�ѧ��ʽ�У�v02��v12=2 a1L
��ã�v1= ![]()
�輴���ŵ����������ľ��ǰ��Lʱ���ٶ�Ϊv���ɶ��ܶ����ɵã�
F��3L���̣�M+m��gL���̣�M+2m��gL���̣�M+3m��gL= ![]() M
M ![]() ��
�� ![]() Mv02��
Mv02��
��ã�v3= ![]()
�𣺵�1��С������Ϻ�ľ���˶���Lʱ��ľ����ٶȴ�СΪ4.9m/s��������С����Ϻ�ľ���˶��˶���Lʱģ����ٶ�Ϊ ![]()
����������1����ʼľ���������˶�����ƽ���������ľ���ܵ��Ļ���Ħ������Ȼ���ɻ���Ħ������ʽ�����Ħ����������2���������ľ���Ϻ�ľ��Ե����ѹ�����ľ���ܵ��Ļ���Ħ���������ţ�ٵڶ�������ü��ٶȣ���3��ÿ�η��������ľ���������Ħ����������ţ�ٵڶ�������ü��ٶȣ������˶�ѧ��ʽ����ٶȣ�Ҳ�����������ľ���Ϻ�ľ��Ե����ѹ�����ľ���ܵ��Ļ���Ħ��������ɶ��ܶ�����������������ϵ�����������ľ��ǰ��Lʱ���ٶȣ�
�����㾫����������Ŀ����֪���������û���Ħ�������ȱ���ֱ���˶����ٶȡ�λ�ơ�ʱ��Ĺ�ϵ�����֪ʶ���Եõ�����Ĵ𰸣���Ҫ���ջ���Ħ����:���ù�ʽf=��F N ���м��㣬����FN ���������ѹ������һ������������������������ܺ�������.���߸���������˶�״̬������ƽ��������ţ�ٶ�������⣻�ٶȹ�ʽ��V=V0+at��λ�ƹ�ʽ��s=v0t+1/2at2���ٶ�λ�ƹ�ʽ��vt2-v02=2as�����ϸ�ʽ��Ϊʸ��ʽ��Ӧ��ʱӦ�涨������Ȼ���ʸ����Ϊ��������⣬ͨ��ѡ���ٶȷ���Ϊ�������Ǹ�������һ�µ�ȡ��+��ֵ�����������෴��ȡ��-��ֵ��