题目内容
如图所示，在粗糙的水平面上，质量分别为m和M(m：M=1：2)的物块A、B用轻弹相连，两物块与水平面间的动摩擦因数相同，当用水平力F作用于B上且两物块共同向右加速运动时，弹簧的伸长量为x1；当用同样的大小的力F竖直加速提升两物块时，弹簧的伸长量为x2，则x1：x2等于（ ）
A．1：1 B．1：2 C．2：1 D．2：3
Ａ
解析试题分析：水平拉系统时，系统加速度为
，弹簧弹力为
，竖直拉系统时，系统加速度为
，弹簧弹力为
，即
，由胡可定律
可知弹簧伸长量相同，选Ａ。
考点：牛顿运动定律的应用
如图所示，倾角为θ的足够长传送带以恒定的速率v0沿逆时针方向运行。t=0时，将质量
m=1kg的小物块（可视为质点）轻放在传送带上，物块速度随时间变化的图象如图所示。设沿传送带向下为正方向，取重力加速度g=10m/s2。则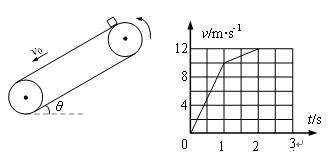
| A．摩擦力的方向始终沿传送带向下 |
| B．1~2s内，物块的加速度为2m/s2 |
| C．传送带的倾角θ=30° |
| D．物体与传送带之间的动摩擦因数μ=0.5 |
如图甲所示，某人正通过定滑轮将质量为m的货物提升到高处．滑轮的质量和摩擦均不计，货物获得的加速度a与绳子对货物竖直向上的拉力T之间的函数关系如图乙所示．由图可以判断 
| A．图线与纵轴的交点M的值aM＝－g |
| B．图线与横轴的交点N的值TN＝mg |
| C．图线的斜率等于物体的质量m |
D．图线的斜率等于物体质量的倒数 |
压敏电阻的阻值随所受压力的增大而减小，有位同学设计了利用压敏电阻判断升降机运动状态的装置，其工作原理如图所示，将压敏电阻固定在升降机底板上，其上放置一个绝缘物块。0～t1时间内升降机停在某一楼层处，t1时刻升降机开始运动，从电流表中得到电流随时间变化的情况如图所示，下列判断正确的是（ ）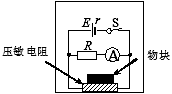
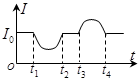
| A．t1时刻升降机开始加速下降 |
| B．t2～t3时间内升降机处于静止状态 |
| C．t3～t4升降机处于超重状态 |
| D．升降机从t1开始，经向上加速、匀速、减速，最后停在较高的楼层处 |
一倾角为30°的斜面上放一木块，木块上固定一支架，支架末端用丝线悬挂一小球，木块在斜面上下滑时，小球与滑块相对静止共同运动。如图所示，下列说法正确的是（ ）
| A．当细线沿竖直方向时，滑块下滑的加速度大小为0 |
B．当细线与斜面方向垂直时，滑块下滑的加速度大小为 |
C．当绳沿水平方向时，滑块下滑的加速度大小为 |
| D．以上说法都不对 |
如图所示，滑轮A可沿倾角为θ的足够长光滑轨道下滑，滑轮下用轻绳挂着一个重为G的物体B，下滑时，物体B相对于A静止，则下滑过程中 （ ）
| A．B的加速度为gsinθ |
B．绳的拉力为 |
| C．绳的方向保持竖直 |
| D．绳的拉力为G |
