题目内容
压敏电阻的阻值随所受压力的增大而减小,有位同学设计了利用压敏电阻判断升降机运动状态的装置,其工作原理如图所示,将压敏电阻固定在升降机底板上,其上放置一个绝缘物块。0~t1时间内升降机停在某一楼层处,t1时刻升降机开始运动,从电流表中得到电流随时间变化的情况如图所示,下列判断正确的是( )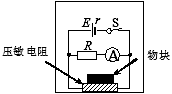
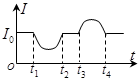
| A.t1时刻升降机开始加速下降 |
| B.t2~t3时间内升降机处于静止状态 |
| C.t3~t4升降机处于超重状态 |
| D.升降机从t1开始,经向上加速、匀速、减速,最后停在较高的楼层处 |
D
解析试题分析:由电流随时间变化的情况可知,0~t1时间内,升降机停在某一楼层处,压敏电阻所受压力 等
等
于绝缘物块的重力 ,即
,即 ;t1~t2时间内,流过电流表的电流变小,由
;t1~t2时间内,流过电流表的电流变小,由 ,则
,则 变小,
变小,
由闭合电路欧姆定律,可知电路中的总电流 变大,则外电路中的并联电阻
变大,则外电路中的并联电阻 变小,
变小,
则压敏电阻的阻值变小,压敏电阻所受压力 增大,即
增大,即 ,由牛顿第二定律可知,物块具有竖直
,由牛顿第二定律可知,物块具有竖直
向上的加速度,则升降机向上做加速运动;t2~t3时间内,压敏电阻所受压力 等于绝缘物块的重力
等于绝缘物块的重力 ,
,
升降机向上做匀速运动;t3~t4时间内,流过电流表的电流变大,则压敏电阻的阻值变大,压敏电阻所受压
力 减小,即
减小,即 ,由牛顿第二定律可知,物块具有竖直向下的加速度,则升降机向上做减速运动,
,由牛顿第二定律可知,物块具有竖直向下的加速度,则升降机向上做减速运动,
升降机处于失重状态,t4时刻,速度减为零,停在较高的楼层处,所以正确选项为D。
考点:本题考查了闭合电路欧姆定律和牛顿第二定律的应用。

 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案一斜块M静止于粗糙的水平面上,在其斜面上放一滑块m,若给m一向下的初速度v0,则m正好保持匀速下滑,如图(6)所示,现在m下滑的过程中再加一个作用力,则以下说法正确的是( )
| A.在m上加一竖直向下的力Fa,则m将保持匀速运动,M对地仍无摩擦力的作用 |
| B.在m上加一沿斜面向下的力Fb,则m将做加速运动,M对地有水平向左的静摩擦力 |
| C.在m上加一水平向右的力Fc,则m将做减速运动,在m停止前M对地仍无摩擦力的作用 |
| D.无论在m上加上什么方向的力,在m停止前M对地都无静摩擦力的作用 |
如图甲所示,一轻杆一端固定在O点,另一端固定一小球,在竖直平面内做半径为R的圆周运动。小球运动到最高点时,杆与小球间弹力大小为N,小球在最高点的速度大小为v,N- 图像如乙图所示。下列说法正确的是( )
图像如乙图所示。下列说法正确的是( )
A.当地的重力加速度大小为 |
B.小球的质量为 |
C.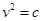 时,杆对小球弹力方向向上 时,杆对小球弹力方向向上 |
D.若 ,则杆对小球弹力大小为 ,则杆对小球弹力大小为 |
如图,某人正通过定滑轮将质量为m的货物提升到高处.滑轮的质量和摩擦均不计,货物获得的加速度a与绳子对货物竖直向上的拉力T之间的函数关系如图所示.由图可以判断正确的是( )
A.图线与纵轴的交点M的值 . . |
B.图线与横轴的交点N的值 . . |
| C.图线的斜率等于物体的质量m. |
| D.图线的斜率等于物体质量的倒数1/m. |
关于速度、加速度、合力间的关系,正确的是( )
| A.物体的速度越大,则物体的加速度越大,所受合力也越大 |
| B.物体的速度为零,则物体的加速度一定为零,所受合力也为零 |
| C.物体的速度为零,加速度可能很大,所受的合力也可能很大 |
| D.物体的速度很大,加速度一定很大,所受的合力可能为零 |
在匀强电场中,有一质量为m,带电量为q的带电小球静止在O点,然后从O点自由释放,其运动轨迹为一直线,直线与竖直方向的夹角为θ,如图所示,那么关于匀强电场的场强大小的下列说法中正确的是:
A.唯一值是 | B.最大值是 |
C.最小值是 | D.不可能是 |

 在以后的运动过程中,圆环运动的速度图象可能是图乙中的( )
在以后的运动过程中,圆环运动的速度图象可能是图乙中的( )
