题目内容
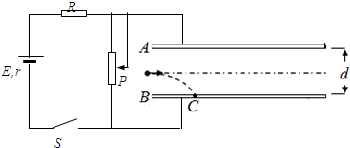
如图所示的电路中,两平行金属板A、B水平放置在竖直平面内,两板间的距离d=40cm.板长为L=1.6m.电源电动势E=24V,内电阻r=1Ω,电阻R=5.3Ω.开关S处于断开状态.此时,一质量为m=4×10-2kg、带电量q=1×10-2C的带负电小球沿两板中心线以某一速度水平射入,该小球射到B板距左端为d的C处.
(1)求小球射入两板时的速度;
(2)调节滑动变阻器滑片,问当闭合开关S后,滑动变阻器接入电路的阻值为多大时,可使同样射入的小球能从A、B板间飞出(不考虑空气阻力,取g=10m/s2)
(1)求小球射入两板时的速度;
(2)调节滑动变阻器滑片,问当闭合开关S后,滑动变阻器接入电路的阻值为多大时,可使同样射入的小球能从A、B板间飞出(不考虑空气阻力,取g=10m/s2)

分析:(1)开关S处于断开状态,小球射入板间做平抛运动,根据平抛运动的规律求解小球射入两板时的速度;
(2)当闭合开关S后,小球将做类平抛运动,小球恰好从A、B板间飞出时偏转距离等于
d,可能向上偏转,也可能向下偏转,根据运动学公式求解加速度大小.根据牛顿第二定律、欧姆定律求解滑动变阻器接入电路的临界阻值,即可得到范围.
(2)当闭合开关S后,小球将做类平抛运动,小球恰好从A、B板间飞出时偏转距离等于
| 1 |
| 2 |
解答:解:(1)开关S处于断开状态,小球射入板间做平抛运动,则有:
d=v0t
d=
gt2
解得:v0=d
=0.4×
=2m/s;
(2)当闭合开关S后,小球将做类平抛运动,小球恰好从A、B板间飞出时偏转距离y=
d
d=
at′2;
l=v0t′
联立解得:a=
m/s2;
若小球恰好从下板飞出时:mg-E1q=ma,
又 E1=
,U1=
E
联立解得:R1=10.5Ω;
同理,若小球恰好从上板飞出时:E2q-mg=ma,E2=
,U2=
联立解得:R2=15.3Ω
所以小球能从A、B板间飞出,R应满足的条件是:10.5Ω<R<15.3Ω.
答:
(1)小球射入两板时的速度是2m/s;
(2)当闭合开关S后,滑动变阻器接入电路的阻值为10.5Ω<R<15.3Ω时,可使同样射入的小球能从A、B板间飞出.
d=v0t
| 1 |
| 2 |
| 1 |
| 2 |
解得:v0=d
|
|
(2)当闭合开关S后,小球将做类平抛运动,小球恰好从A、B板间飞出时偏转距离y=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
l=v0t′
联立解得:a=
| 5 |
| 8 |
若小球恰好从下板飞出时:mg-E1q=ma,
又 E1=
| U1 |
| d |
| R1 |
| R1+R+r |
联立解得:R1=10.5Ω;
同理,若小球恰好从上板飞出时:E2q-mg=ma,E2=
| U2 |
| d |
| R2 |
| R2+R+r |
联立解得:R2=15.3Ω
所以小球能从A、B板间飞出,R应满足的条件是:10.5Ω<R<15.3Ω.
答:
(1)小球射入两板时的速度是2m/s;
(2)当闭合开关S后,滑动变阻器接入电路的阻值为10.5Ω<R<15.3Ω时,可使同样射入的小球能从A、B板间飞出.
点评:本题中平抛运动与类平抛运动的研究方法相同,都运动的分解法,对于类平抛运动与电路之间联系的纽带是板间的电压,要能熟练通过欧姆定律和电路连接关系得到板间电压.

练习册系列答案
相关题目
 如图所示的电路中,两平行金属板A、B水平放置,极板长l=80cm,两板间的距离d=40cm.电源电动势E=40V,内电阻r=1Ω,电阻R=15Ω,闭合开关S,待电路稳定后,将一带负电的小球从B板左端且非常靠近B板的位置以初速度v0=4m/s水平向右射入两板间,该小球可视为质点.若小球带电量q=1×10-2 C,质量为m=2×10-2 kg,不考虑空气阻力,电路中电压表、
如图所示的电路中,两平行金属板A、B水平放置,极板长l=80cm,两板间的距离d=40cm.电源电动势E=40V,内电阻r=1Ω,电阻R=15Ω,闭合开关S,待电路稳定后,将一带负电的小球从B板左端且非常靠近B板的位置以初速度v0=4m/s水平向右射入两板间,该小球可视为质点.若小球带电量q=1×10-2 C,质量为m=2×10-2 kg,不考虑空气阻力,电路中电压表、 如图所示的电路中,两平行金属板A、B水平放置,两板间的距离d=40cm.电源电动势E=24V,内阻r=1Ω,电阻R=15Ω.闭合开关S,待电路稳定后,将一带正电的小球从B板小孔以初速度v0=4m/s竖直向上射入板间.若小球电荷量为q=1×10-2 C,质量为m=2×10-2 kg,不考虑空气阻力.( 取g=10m/s2),求
如图所示的电路中,两平行金属板A、B水平放置,两板间的距离d=40cm.电源电动势E=24V,内阻r=1Ω,电阻R=15Ω.闭合开关S,待电路稳定后,将一带正电的小球从B板小孔以初速度v0=4m/s竖直向上射入板间.若小球电荷量为q=1×10-2 C,质量为m=2×10-2 kg,不考虑空气阻力.( 取g=10m/s2),求 在如图所示的电路中,两个灯泡均发光,当滑动变阻器的滑动头向下滑动时,则( )
在如图所示的电路中,两个灯泡均发光,当滑动变阻器的滑动头向下滑动时,则( ) 6、如图所示的电路中,两支路的电阻相等,流过电流表A1的电流强度为I1,流过电流表A2的电流强度为I2,则在接通开关S和断开开关S的瞬间,观察到的现象是 ( )
6、如图所示的电路中,两支路的电阻相等,流过电流表A1的电流强度为I1,流过电流表A2的电流强度为I2,则在接通开关S和断开开关S的瞬间,观察到的现象是 ( ) 如图所示的电路中,两平行金属板A、B水平放置,两板间的距离d=40cm.电路电压恒为U=24V,电阻R=16Ω.闭合开关S,待电路稳定后,将一带正电的小球从B板小孔以初速度v0=4m/s竖直向上射入板间.若小球带电荷量为q=1×10-2C,质量为m=2×10-2kg,不考虑空气阻力.求:
如图所示的电路中,两平行金属板A、B水平放置,两板间的距离d=40cm.电路电压恒为U=24V,电阻R=16Ω.闭合开关S,待电路稳定后,将一带正电的小球从B板小孔以初速度v0=4m/s竖直向上射入板间.若小球带电荷量为q=1×10-2C,质量为m=2×10-2kg,不考虑空气阻力.求: