题目内容
3.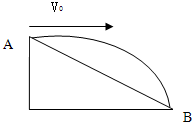 如图所示,AB为倾角θ=37°的斜面,小球从A点以初速度V0=10m/s水平抛出,恰好落到B点,不计空气阻力,g=10m/s2.
如图所示,AB为倾角θ=37°的斜面,小球从A点以初速度V0=10m/s水平抛出,恰好落到B点,不计空气阻力,g=10m/s2.求:(1)AB间的距离XAB
(2)小球在空中飞行的时间
(3)经多长时间石子离斜面的距离最远.
分析 根据水平位移和竖直位移的关系,结合运动学公式求出小球在空中的时间,根据初速度和时间求出水平位移,从而根据平行四边形定则求出AB间的距离.
根据平行四边形定则求出石子与斜面平行时的竖直分速度,结合速度时间公式求出运动的时间.
解答 解:(2)小球做平抛运动,tan37°=$\frac{y}{x}$=$\frac{\frac{1}{2}g{t}^{2}}{{v}_{0}t}$=$\frac{gt}{2{v}_{0}}$,解得:t=1.5s;
(1)AB间的距离:XAB=$\frac{x}{cos37°}$=$\frac{{v}_{0}t}{cos37°}$=18.75m;
(3)当石子垂直于斜面的分为零时石子离斜面的距离最远,
时间:t′=$\frac{{v}_{0}sin37°}{gcos37°}$=0.75s;
答:(1)AB间的距离XAB为18.75m;
(2)小球在空中飞行的时间为1.5s;
(3)经时间0.75s石子离斜面的距离最远.
点评 解决本题的关键知道平抛运动在水平方向和竖直上的运动规律,结合运动学公式灵活求解,难度不大.

练习册系列答案
相关题目
8. 如图所示的电路中,电源电动势为E、内电阻为r.将滑动变阻器的滑片P从图示位置向右滑动的过程中,关于各电表示数的变化,下列判断中正确的是( )
如图所示的电路中,电源电动势为E、内电阻为r.将滑动变阻器的滑片P从图示位置向右滑动的过程中,关于各电表示数的变化,下列判断中正确的是( )
 如图所示的电路中,电源电动势为E、内电阻为r.将滑动变阻器的滑片P从图示位置向右滑动的过程中,关于各电表示数的变化,下列判断中正确的是( )
如图所示的电路中,电源电动势为E、内电阻为r.将滑动变阻器的滑片P从图示位置向右滑动的过程中,关于各电表示数的变化,下列判断中正确的是( )| A. | 电压表V的示数变小 | B. | 电流表A3的示数变小 | ||
| C. | 电流表A2的示数变小 | D. | 电流表A1的示数变大 |
13.关于位移和路程,下列说法不正确的是( )
| A. | 质点的位移是矢量,路程是标量 | |
| B. | 质点通过的路程不等,但位移可能相等 | |
| C. | 质点通过的路程不为零,但位移可能是零 | |
| D. | 质点做直线运动且运动方向始终不变时,那么它通过的路程就是位移 |
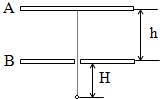 水平放置的两平行金属板相距h,有一质量为m、电荷量为+q的小球在B板 小孔正下方H处以初速度v0竖直向上进入两板之间,欲使小球恰好打到A板,已知板间匀强电场为E,求v0的大小?
水平放置的两平行金属板相距h,有一质量为m、电荷量为+q的小球在B板 小孔正下方H处以初速度v0竖直向上进入两板之间,欲使小球恰好打到A板,已知板间匀强电场为E,求v0的大小? F1和F2是F的两个分力,其中,F=20N,F1=12N.F和F1的方向如图所示,试用作图法求出另一个分力F2的大小.
F1和F2是F的两个分力,其中,F=20N,F1=12N.F和F1的方向如图所示,试用作图法求出另一个分力F2的大小.
 如图所示,长为L的轻绳一端系于固定点O,另一端系质量为m的小球,将小球从O点正下放$\frac{L}{4}$处,以一定初速度水平向右抛出,经一定时间绳被拉直以后,小球将以O为圆心在竖直平面内摆动,已知绳刚被拉直时,绳与竖直线成60°,如图,求
如图所示,长为L的轻绳一端系于固定点O,另一端系质量为m的小球,将小球从O点正下放$\frac{L}{4}$处,以一定初速度水平向右抛出,经一定时间绳被拉直以后,小球将以O为圆心在竖直平面内摆动,已知绳刚被拉直时,绳与竖直线成60°,如图,求