Question

“嫦娥一号”和“嫦娥二号”月球探测卫星的圆形绕月轨道距月球表面分别约为200 km和100 km．当它们在绕月轨道上运行时，两者相比，“嫦娥二号”的

A．周期较小                             B．线速度较小

C．角速度较小                           D．向心加速度较小

 

Answer 1

【答案】

A

【解析】

试题分析：根据月球对嫦娥卫星的万有引力提供向心力，可分别得到周期、线速度、角速度、向心加速度与轨道半径的关系来分析．

设月球的质量为M，嫦娥卫星的质量为m，轨道半径为r．

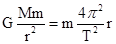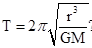A、由，得到，可知“嫦娥二号”环月运行的周期比“嫦娥一号”更小．故A正确．

B、由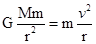，得到可知，“嫦娥二号”环月运行时的线速度比“嫦娥一号”更大．故B错误．

C、由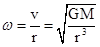可知，“嫦娥二号”环月运行时的角速度比“嫦娥一号”更大．故C错误．

D、由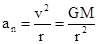可知，“嫦娥二号”环月运行时的向心加速度比“嫦娥一号”更大．故D错误．

故选A.

考点：人造卫星的加速度、周期和轨道的关系．

点评：本题考查运用万有引力定律与圆周运动知识解决实际问题的能力，要灵活选择公式的形式．