题目内容
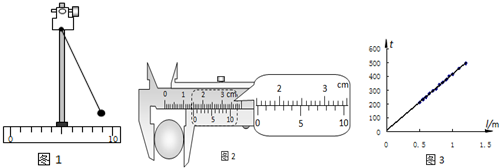
某同学利用如图1所示的装置测量当地的重力加速度.实验步骤如下:

A.按装置图安装好实验装置;
B.用游标卡尺测量小球的直径d;
C.用米尺测量悬线的长度l;
D.让小球在竖直平面内小角度摆动.
当小球经过最低点时开始计时,并计数为0,此后小球每经过最低点一次,依次计数1、2、3….当数到20时,停止计时,测得时间为t;
E.多次改变悬线长度,重复实验步骤C、D;
F.计算出每个悬线长度对应的t2;
G.以t2为纵坐标、l为横坐标,作出t2-l图线.
结合上述实验,完成下列任务:
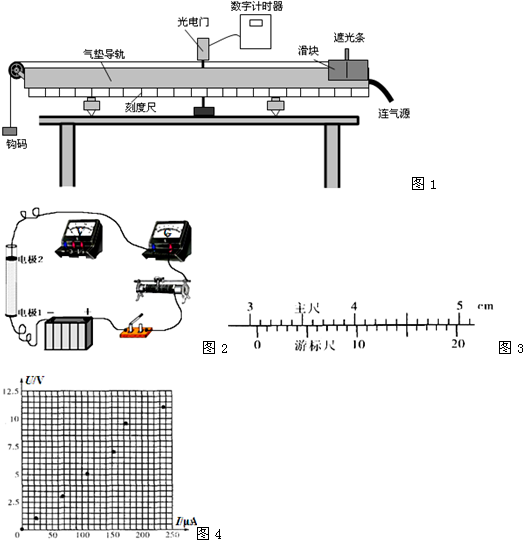
(1)用游标为10分度的卡尺测量小球的直径.某次测量的示数如图2所示,读出小球直径d的值为
(2)该同学根据实验数据,利用计算机作出t2-l图线如图4所示.根据图线拟合得到方程t 2=404.0l+3.0.由此可以得出当地的重力加速度g=
(3)从理论上分析图线没有过坐标原点的原因,下列分析正确的是
A.不应在小球经过最低点时开始计时,应该在小球运动到最高点开始计时;
B.开始计时后,不应记录小球经过最低点的次数,而应记录小球做全振动的次数;
C.不应作t2-l图线,而应作t-l图线;
D.不应作t2-l图线,而应作t 2-(l+
)图线.

A.按装置图安装好实验装置;
B.用游标卡尺测量小球的直径d;
C.用米尺测量悬线的长度l;
D.让小球在竖直平面内小角度摆动.
当小球经过最低点时开始计时,并计数为0,此后小球每经过最低点一次,依次计数1、2、3….当数到20时,停止计时,测得时间为t;
E.多次改变悬线长度,重复实验步骤C、D;
F.计算出每个悬线长度对应的t2;
G.以t2为纵坐标、l为横坐标,作出t2-l图线.
结合上述实验,完成下列任务:
(1)用游标为10分度的卡尺测量小球的直径.某次测量的示数如图2所示,读出小球直径d的值为
1.52
1.52
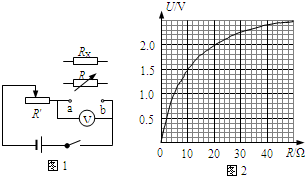
cm;用秒表记录了单摆振动多次所用的时间(如图3),秒表所示读数为99.8
99.8
s;(2)该同学根据实验数据,利用计算机作出t2-l图线如图4所示.根据图线拟合得到方程t 2=404.0l+3.0.由此可以得出当地的重力加速度g=
9.76
9.76
m/s2.(取π 2=9.86,结果保留3位有效数字)(3)从理论上分析图线没有过坐标原点的原因,下列分析正确的是
D
D
A.不应在小球经过最低点时开始计时,应该在小球运动到最高点开始计时;
B.开始计时后,不应记录小球经过最低点的次数,而应记录小球做全振动的次数;
C.不应作t2-l图线,而应作t-l图线;
D.不应作t2-l图线,而应作t 2-(l+
| d | 2 |
分析:①游标卡尺主尺与游标尺示数之和是游标卡尺的示数.秒表先读分针读数,再读秒针读数,两者相加
②根据单摆周期公式求出t2-l函数关系式,然后求出重力加速度.
③单摆摆长等于摆线长度与摆球半径之和,以摆线长度作为摆长,则摆长偏小.
②根据单摆周期公式求出t2-l函数关系式,然后求出重力加速度.
③单摆摆长等于摆线长度与摆球半径之和,以摆线长度作为摆长,则摆长偏小.
解答:解:(1)由图示游标卡尺可知,主尺示数是1.5cm,游标尺示数是2×0.1mm=0.2mm=0.02cm,
游标卡尺示数即小球的直径d=1.5cm+0.02cm=1.52cm;
用秒表记录了单摆振动多次所用的时间(如图3),
秒表所示读数为90s+9.8s=99.8s.
(2)由题意知,单摆的周期T=
=
由单摆周期公式T=2π
可得:t2=
l,
由图象得到的方程为:t2=404.0l+3.0,
则
=404.0,
g=
≈9.76m/s2;
(3)单摆摆长等于摆线长度与摆球半径之和,把摆线长度作为单摆摆长,
摆长小于实际摆长,t2-l图象不过原点,在纵轴上截距不为零,故D正确,
故选:D
故答案为:(1)1.52,99.8 (2)9.76 (3)D
游标卡尺示数即小球的直径d=1.5cm+0.02cm=1.52cm;
用秒表记录了单摆振动多次所用的时间(如图3),
秒表所示读数为90s+9.8s=99.8s.
(2)由题意知,单摆的周期T=
| t | ||
|
| t |
| 10 |
由单摆周期公式T=2π
|
| 400π2 |
| g |
由图象得到的方程为:t2=404.0l+3.0,
则
| 400π2 |
| g |
g=
| 400π2 |
| 404.0 |
(3)单摆摆长等于摆线长度与摆球半径之和,把摆线长度作为单摆摆长,
摆长小于实际摆长,t2-l图象不过原点,在纵轴上截距不为零,故D正确,
故选:D
故答案为:(1)1.52,99.8 (2)9.76 (3)D
点评:常用仪器的读数要掌握,这是物理实验的基础.掌握单摆的周期公式,从而求解加速度

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目

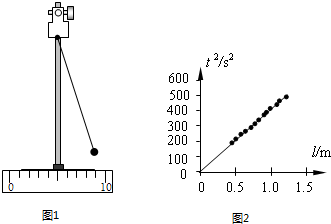 (2009?上海模拟)某同学利用如图1所示的装置测量当地的重力加速度.实验步骤如下:
(2009?上海模拟)某同学利用如图1所示的装置测量当地的重力加速度.实验步骤如下: