题目内容
3.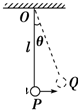 如图所示,一个质量为m的小球用长为l的轻绳悬挂于O点,小球在水平拉恒力F的作用下,从平衡位置P点很缓慢地移动到Q点,则水平力F所做的功为( )
如图所示,一个质量为m的小球用长为l的轻绳悬挂于O点,小球在水平拉恒力F的作用下,从平衡位置P点很缓慢地移动到Q点,则水平力F所做的功为( )| A. | mglcosθ | B. | Flsinθ | C. | mgl(1-cosθ) | D. | Fl(1-cosθ) |
分析 小球在水平拉力F的作用下,从平衡位置P点很缓慢地移动到Q点,动能不变,根据动能定理求出水平力F所做的功.
解答 解:小球在缓慢移动的过程中,水平力F是变力,不能通过功的公式求解功的大小,根据动能定理得:WF-mgl(1-cosθ)=0,
解得水平力F所做的功为:WF=mgl(1-cosθ).故C正确,A、B、D错误.
故选:C.
点评 本题考查了动能定理的基本运用,运用动能定理解题,首先要确定研究的过程,分析在过程中有哪些力做功,然后根据动能定理列式求解.

练习册系列答案
相关题目
13.放在光滑水平面上的物体,受到和水平面成60°角的斜向上的拉力作用2s钟,获得动量为40kg•m/s(物体没有离开地面).这个拉力大小为( )
| A. | 80N | B. | 40N | C. | 34.6N | D. | 20N |
14.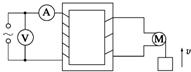 如图所示,理想变压器的原线圈接正弦交变电流,副线圈接电动机,原、副线圈的匝数比n1:n2=2:1,电动机线圈电阻为R.当输入端接通电源后,理想电流表读数为I,电动机带动一质量为m的重物以速度v匀速上升.若电动机因摩擦造成的能量损失不计,则图中电压表的读数为( )
如图所示,理想变压器的原线圈接正弦交变电流,副线圈接电动机,原、副线圈的匝数比n1:n2=2:1,电动机线圈电阻为R.当输入端接通电源后,理想电流表读数为I,电动机带动一质量为m的重物以速度v匀速上升.若电动机因摩擦造成的能量损失不计,则图中电压表的读数为( )
 如图所示,理想变压器的原线圈接正弦交变电流,副线圈接电动机,原、副线圈的匝数比n1:n2=2:1,电动机线圈电阻为R.当输入端接通电源后,理想电流表读数为I,电动机带动一质量为m的重物以速度v匀速上升.若电动机因摩擦造成的能量损失不计,则图中电压表的读数为( )
如图所示,理想变压器的原线圈接正弦交变电流,副线圈接电动机,原、副线圈的匝数比n1:n2=2:1,电动机线圈电阻为R.当输入端接通电源后,理想电流表读数为I,电动机带动一质量为m的重物以速度v匀速上升.若电动机因摩擦造成的能量损失不计,则图中电压表的读数为( )| A. | 4IR+$\frac{mgv}{I}$ | B. | $\frac{mgv}{I}$ | C. | 4IR | D. | $\frac{1}{4}$IR+$\frac{mgv}{I}$ |
11.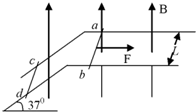 两根相距为L的足够长的金属弯角光滑导轨如图所示放置,它们各有一边在同一水平面内,另一边与水平面的夹角为37°,质量均为m的金属细杆ab、cd与导轨垂直接触形成闭合回路,导轨的电阻不计,回路总电阻为2R,整个装置处于磁感应强度大小为B,方向竖直向上的匀强磁场中,当ab杆在平行于水平导轨的拉力F作用下以速度v沿导轨匀速运动时,cd杆恰好处于静止状态,重力加速度为g,以下说法正确的是( )
两根相距为L的足够长的金属弯角光滑导轨如图所示放置,它们各有一边在同一水平面内,另一边与水平面的夹角为37°,质量均为m的金属细杆ab、cd与导轨垂直接触形成闭合回路,导轨的电阻不计,回路总电阻为2R,整个装置处于磁感应强度大小为B,方向竖直向上的匀强磁场中,当ab杆在平行于水平导轨的拉力F作用下以速度v沿导轨匀速运动时,cd杆恰好处于静止状态,重力加速度为g,以下说法正确的是( )
 两根相距为L的足够长的金属弯角光滑导轨如图所示放置,它们各有一边在同一水平面内,另一边与水平面的夹角为37°,质量均为m的金属细杆ab、cd与导轨垂直接触形成闭合回路,导轨的电阻不计,回路总电阻为2R,整个装置处于磁感应强度大小为B,方向竖直向上的匀强磁场中,当ab杆在平行于水平导轨的拉力F作用下以速度v沿导轨匀速运动时,cd杆恰好处于静止状态,重力加速度为g,以下说法正确的是( )
两根相距为L的足够长的金属弯角光滑导轨如图所示放置,它们各有一边在同一水平面内,另一边与水平面的夹角为37°,质量均为m的金属细杆ab、cd与导轨垂直接触形成闭合回路,导轨的电阻不计,回路总电阻为2R,整个装置处于磁感应强度大小为B,方向竖直向上的匀强磁场中,当ab杆在平行于水平导轨的拉力F作用下以速度v沿导轨匀速运动时,cd杆恰好处于静止状态,重力加速度为g,以下说法正确的是( )| A. | ab杆所受拉力F的大小为mgtan37° | |
| B. | 回路中电流为$\frac{mgtan37°}{BL}$ | |
| C. | 回路中电流的总功率为mgvsin37° | |
| D. | m与v大小的关系为m=$\frac{{B}^{2}{L}^{2}v}{2Rgtan37°}$ |
15.对万有引力定律的表达式F=G$\frac{{m}_{1}{m}_{2}}{{r}^{2}}$的认识,下列说法错误的是( )
| A. | 公式中G为引力常量,它是由实验测得的,而不是人为规定的 | |
| B. | 当m1与m2一定时,随着r的增大,万有引力逐渐减小 | |
| C. | 质量分别为m1和m2的两物体之间的引力大小相等、方向相反,是一对平衡力 | |
| D. | 质量分别为m1和m2的两物体受到的引力总是大小相等,与m1、m2是否相等无关 |
13.下列两个核反应构成所谓${\;}_{1}^{3}$H-${\;}_{1}^{2}$H(${\;}_{3}^{6}$Li)燃料循环,式中X、Y为生成的核或粒子,E1、E2为释放的能量:${\;}_{3}^{6}$Li+${\;}_{0}^{1}$n→X+${\;}_{2}^{4}$He+E1,${\;}_{1}^{2}$H+${\;}_{1}^{3}$H→${\;}_{2}^{4}$He+Y+E2,锂核、氘核和α粒子的质量分别为mLi、mD、mα,则( )
| A. | (mLi+mD-2mα)c2=E1+E2 | B. | (mLi+mD-mα)c2=E1+E2 | ||
| C. | 2(mLi+mD-mα)c2=E1+E2 | D. | (mLi+2mD-mα)c2=E1+E2 |
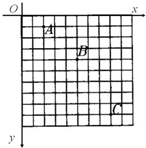 如图为某小球做平抛运动时,用闪光照相的方法获得的相片的一部分,图中背景方格的边长为5cm,g=10m/s2,并把这一部分放在图中的坐标系内,则:
如图为某小球做平抛运动时,用闪光照相的方法获得的相片的一部分,图中背景方格的边长为5cm,g=10m/s2,并把这一部分放在图中的坐标系内,则:
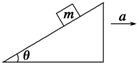 如图所示,质量为m的木块置于斜面上,木块与斜面间的动摩擦因数为μ,在外力作用下,斜面以加速度a沿水平方向向右做匀加速运动,运动中物体m与斜面体相对静止.则木块受到的重力不做功,受到的支持力做负功,受到的摩擦力做正功(填“正功”,“负功”或“不做功”)
如图所示,质量为m的木块置于斜面上,木块与斜面间的动摩擦因数为μ,在外力作用下,斜面以加速度a沿水平方向向右做匀加速运动,运动中物体m与斜面体相对静止.则木块受到的重力不做功,受到的支持力做负功,受到的摩擦力做正功(填“正功”,“负功”或“不做功”)