题目内容
11.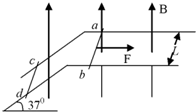 两根相距为L的足够长的金属弯角光滑导轨如图所示放置,它们各有一边在同一水平面内,另一边与水平面的夹角为37°,质量均为m的金属细杆ab、cd与导轨垂直接触形成闭合回路,导轨的电阻不计,回路总电阻为2R,整个装置处于磁感应强度大小为B,方向竖直向上的匀强磁场中,当ab杆在平行于水平导轨的拉力F作用下以速度v沿导轨匀速运动时,cd杆恰好处于静止状态,重力加速度为g,以下说法正确的是( )
两根相距为L的足够长的金属弯角光滑导轨如图所示放置,它们各有一边在同一水平面内,另一边与水平面的夹角为37°,质量均为m的金属细杆ab、cd与导轨垂直接触形成闭合回路,导轨的电阻不计,回路总电阻为2R,整个装置处于磁感应强度大小为B,方向竖直向上的匀强磁场中,当ab杆在平行于水平导轨的拉力F作用下以速度v沿导轨匀速运动时,cd杆恰好处于静止状态,重力加速度为g,以下说法正确的是( )| A. | ab杆所受拉力F的大小为mgtan37° | |
| B. | 回路中电流为$\frac{mgtan37°}{BL}$ | |
| C. | 回路中电流的总功率为mgvsin37° | |
| D. | m与v大小的关系为m=$\frac{{B}^{2}{L}^{2}v}{2Rgtan37°}$ |
分析 ab杆和cd杆均处于平衡状态,运用平衡条件分别对两杆研究,即可求得F的大小;对于cd杆分析,由平衡条件求解感应电流;回路中电流的总功率等于拉力的功率,由公式P=Fv求出.根据安培力与速度的关系,推导出m与v的关系.
解答 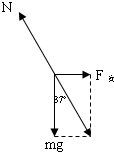 解:A、对于cd杆,分析受力如图,根据平衡条件得:F安=mgtan37°;对ab杆,由于感应电流的大小、导线的长度相等,两杆所受的安培力大小相等,由平衡条件得知,F=F安,则得:F=mg tan37°.故A正确.
解:A、对于cd杆,分析受力如图,根据平衡条件得:F安=mgtan37°;对ab杆,由于感应电流的大小、导线的长度相等,两杆所受的安培力大小相等,由平衡条件得知,F=F安,则得:F=mg tan37°.故A正确.
B、cd杆所受的安培力F安=BIL,又F安=mgtan37°,则得电流为 I=$\frac{mgtan37°}{BL}$,故B正确.
C、回路中电流的总功率等于拉力的功率,为P=Fv=mgvtan37°,故C错误.
D、根据E=BLv,I=$\frac{E}{2R}$,F安=BIL得,F安=$\frac{{B}^{2}{L}^{2}v}{2R}$,结合F安=mgtan37°,得:m=$\frac{{B}^{2}{L}^{2}v}{2Rgtan37°}$.故D正确.
故选:ABD
点评 本题要熟练运用法拉第电磁感应定律、平衡方程等规律,强调受力分析的正确性,同时突出克服安培力所做的功等于产生的焦耳热.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.设土星绕太阳的运动是匀速圆周运动,若测得土星到太阳的距离是r,土星绕太阳运动的周期是T,万有引力常量G已知,根据这些数据无法求出的量是( )
| A. | 土星的线速度大小 | B. | 土星的向心力大小 | ||
| C. | 土星的质量 | D. | 太阳的质量 |
6.肩负我国首次太空行走运载任务的神舟七号飞船,在绕地球五圈后成功的由椭圆轨道变成圆形轨道,在圆形轨道上,飞船离地面的距离约为350千米,绕行周期约为90分钟,设飞船在圆形轨道上的运动为匀速圆周运动,下述说法正确的是( )
| A. | 地球对飞船的引力大于飞船绕地球做匀速圆周运动的向心力 | |
| B. | 飞船内的物体处于失重状态,不受地球引力 | |
| C. | 飞船在圆形轨道上运动的线速度大小一定小于7.9km/s | |
| D. | 它离地面越高,其绕行速度一定越大 |
16.在经典力学的建立过程中,牛顿和伽利略均作出了重要贡献.下列说法正确的是( )
| A. | 伽利略总结出了惯性定律 | |
| B. | 牛顿提出了牛顿三大定律 | |
| C. | 伽利略总结得出作用力和反作用力之间的关系 | |
| D. | 牛顿利用理想实验推断出匀速运动需要力来维持 |
3.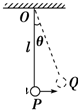 如图所示,一个质量为m的小球用长为l的轻绳悬挂于O点,小球在水平拉恒力F的作用下,从平衡位置P点很缓慢地移动到Q点,则水平力F所做的功为( )
如图所示,一个质量为m的小球用长为l的轻绳悬挂于O点,小球在水平拉恒力F的作用下,从平衡位置P点很缓慢地移动到Q点,则水平力F所做的功为( )
 如图所示,一个质量为m的小球用长为l的轻绳悬挂于O点,小球在水平拉恒力F的作用下,从平衡位置P点很缓慢地移动到Q点,则水平力F所做的功为( )
如图所示,一个质量为m的小球用长为l的轻绳悬挂于O点,小球在水平拉恒力F的作用下,从平衡位置P点很缓慢地移动到Q点,则水平力F所做的功为( )| A. | mglcosθ | B. | Flsinθ | C. | mgl(1-cosθ) | D. | Fl(1-cosθ) |
20.下列说法正确的是( )
| A. | 法拉第发现了电磁感应现象 | |
| B. | 紫外线比红外线更容易产生显著的衍射现象 | |
| C. | 根据麦克斯韦电磁场理论,变化的电场周围一定产生变化的磁场 | |
| D. | 质量相同的物体,速度大的惯性大 |
1.关于重力势能,以下说法中正确的是( )
| A. | 某个物体处于某个位置,重力势能的大小是唯一确定的 | |
| B. | 物体克服重力做功重力势能减少 | |
| C. | 只要重力做功,物体的重力势能一定变化 | |
| D. | 物体做匀速直线运动时,其重力势能一定不变 |
 如图,质量为0.5kg的小桶里盛有1kg的水,用绳子系住小桶在竖直平面内绕O点做“水流星”表演,转动半径为2m,小桶通过最低点的速度为12m/s.(计算中取g=10m/s2)求:
如图,质量为0.5kg的小桶里盛有1kg的水,用绳子系住小桶在竖直平面内绕O点做“水流星”表演,转动半径为2m,小桶通过最低点的速度为12m/s.(计算中取g=10m/s2)求: