题目内容
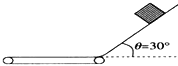
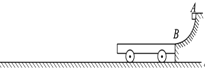
【题目】如图所示,AB为半径R=0.8 m的1/4光滑圆弧轨道,下端B恰与小车右端平滑对接.小车质量M=3 kg,车长L=2.06 m.现有一质量m=1 kg的滑块,由轨道顶端无初速释放,滑到B端后冲上小车.当车运行了2 s时,车被地面装置锁定.已知地面光滑,滑块与小车上表面间的动摩擦因数μ=0.3, g取10 m/s2.试求:
(1)滑块到达B端时,它对轨道的压力大小;
(2)从车开始运动到被锁定的过程中,摩擦力对滑块所做的功;
(3)滑块离开车时的动能.
【答案】(1) 30 N(2)-7.5J(3)0.32J
【解析】
(1)滑块从光滑圆弧轨道过程,根据机械能守恒定律得:mgR=![]() mv2
mv2
解得v=4m/s
滑块经过B端时,由牛顿第二定律得:N-mg=m![]()
联立两式,代入数值得,轨道对滑块的支持力为:N=3mg=3×1×10=30N
(2)当滑块滑上小车后,由牛顿第二定律,得
对滑块有:-μmg=ma1
对小车有:umg=Ma2
设经时间t两者达到共同速度,则有:v+a1t=a2t
解得t=1s.由于1s<2s,此时小车还未被锁定,两者的共同速度:v′=a2t=1m/s,两者以共同速度运动时间为t′=1s.
此过程中,滑块的位移![]()
摩擦力对滑块所做的功:![]()
(3)两者达到共速时小车的位移![]() ,
,
此时物块距离小车的左端L1=2.06-(2.5-0.5)=0.06m
然后小车被锁定后,滑块以v′= 1m/s的速度做匀减速运动,加速度为a1=-μg=-3m/s2,
则滑离小车时的速度:![]()
动能为![]()

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目