题目内容
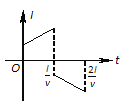
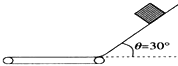
【题目】如图所示,一倾角为30°的光滑斜面,下端与一段很短的光滑弧面相切,弧面另一端与水平传送带相切,水平传送带以5 m/s的速度顺时针转动。现有质量为1 kg的物体(视为质点)从斜面上距传送带高h=5 m处由静止滑下;物体在弧面运动时不损失机械能,而且每次在弧面上运动的时间可以忽略。已知传送带足够长,它与物体之间的动摩擦因数为0.5,取g=10 m/s2,则
A. 物体第一次刚滑上水平传送带时的速度大小为5 m/s
B. 物体从第一次滑上传送带到第一次离开传送带所用的时间为4.5 s
C. 物体从第一次滑上传送带到第一次离开传送带的过程中,摩擦产生的热量为200 J
D. 物体从第一次滑上传送带到第一次离开传送带的过程中,摩擦力对物体做的功为-37.5 J
【答案】BD
【解析】
A.物体由光滑斜面下滑的过程,只有重力做功,根据机械能守恒求解物体到斜面末端的速度大小;
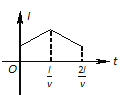
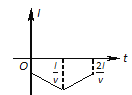
B、当物体滑到传送带最左端速度为零时,AB间的距离L最小,由位移公式求出物块向左的时间;随后物块先向右加速到速度等于5m/s,然后做匀速直线运动,由运动学的公式分别求出各段的时间,然后求和;
C、摩擦产生的热量等于摩擦力与相对位移的乘积,由此即可求出;
D、根据动能定理求解即可.
A. 物体由光滑斜面下滑的过程,只有重力做功,机械能守恒,则得:mgh=![]() mv2
mv2
解得:v= ![]() m/s=10m/s.故A错误;
m/s=10m/s.故A错误;
B. 当物体滑到传送带最左端速度为零时,AB间的距离L最小,
物块在传送带上的加速度:a=μmg/m=μg=0.5×10=5m/s2
物块到速度等于0的时间:t1= ![]() s=2s
s=2s
物块的位移:L=![]() m=10m
m=10m
物块的速度等于0后,随传送带先向右做加速运动,加速度的大小不变,则物块达到与传送带速度相等的时间:
t2=v0/a=5/5=1s
位移:x1= ![]() m=2.5m
m=2.5m
物块随传送带做匀速直线运动的时间:t3= ![]() s=1.5s
s=1.5s
所以物体从第一次滑上传送带到第一次离开传送带所用的时间为:t=t1+t2+t3=2+1+1.5=4.5s.故B正确;
C. 物块向左做减速运动的过程中,传送带的位移:x2=v0t1=5×2=10m
物块向右加速的过程中传送带的位移:x3=v0t2=5×1=5m
相对位移:△x=L+x2+x3x1=10+10+52.5=22.5m,
该过程中产生的热量:Q=μmg△x=0.5×1×10×22.5=112.5J.故C错误;
D. 由动能定理得:Wf= ![]()
解得:Wf=37.5J.故D正确。
故选:BD