��Ŀ����
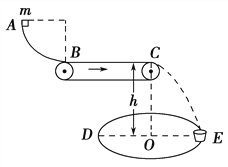
����Ŀ��ͼ����ʾ�������������������������̫���и������������Dz�����Դ���ӳ����ǵ�ʹ��������ͼ�������������������ij������һ�ŵ���ͬ������ǰ��������ͬһƽ��������ͬ���з����Ƶ���������Բ���˶���ʾ��ͼ����ʱ���ߵ�����ͨ�����ġ�����뾶֮��Ϊ1:4.���������������������������֮���������������˵����ȷ����

A.��ͼʾ�����,����������������ٶȴ���![]()
B.��ͼʾ�����,��������������ļ��ٶȴ�С�ǵ���ͬ�����ǵ�4��
C.��ͼʾ�����,�������������������Ϊ3h���Ҵ�ͼʾλ�ÿ�ʼ��1.5h��ͬ�����ǵľ������
D.��Ҫ�Ը�ͬ������ʵʩ����,�������������Ӧ��ͼʾ����ϼ��٣�Ȼ����ͬ�����ǶԽ�
���𰸡�D
��������
���������A.��![]() ֪��һ�����ٶ������ǵ���������ٶ�,����������������ٶ�һ��С��7.9km/s����A����B.��ţ�ٵڶ����ɿɵ�
֪��һ�����ٶ������ǵ���������ٶ�,����������������ٶ�һ��С��7.9km/s����A����B.��ţ�ٵڶ����ɿɵ�![]() �����ߵĹ���뾶֮��Ϊ1��4�����Լ��ٶȱ�Ϊ16��1����B����C.�����Ǵ������Զ��������������
�����ߵĹ���뾶֮��Ϊ1��4�����Լ��ٶȱ�Ϊ16��1����B����C.�����Ǵ������Զ��������������![]() ��
��![]() ����C����D.���������������ͼʾ����ϼ��٣�����������˶����Ӷ��ӽ�ͬ���������ʵ�ֶԽӣ���D��ȷ��
����C����D.���������������ͼʾ����ϼ��٣�����������˶����Ӷ��ӽ�ͬ���������ʵ�ֶԽӣ���D��ȷ��

 A�ӽ��� ϵ�д�
A�ӽ��� ϵ�д� ȫ�Ų��Ծ�ϵ�д�
ȫ�Ų��Ծ�ϵ�д�