题目内容
【题目】如图所示，在磁感应强度大小为B、方向垂直纸面向里的匀强磁场中有一粒子源，粒子源从O点在纸面内均匀地向各个方向同时发射速率为v的带电粒子（质量为m，电荷量为＋q）、PQ是在纸面内垂直磁场放置的挡板（厚度不计，长度足够），挡板的P端与O点的连线与挡板垂直，距离为
，且粒子打在挡板两侧都会被吸收，不计带电粒子的重力与粒子间的相互作用，磁场分布足够大，求：
（1）水平向右出射的粒子所打挡板位置和P点的距离L；
（2）打在挡板右侧的粒子在磁场中运动时间的最大差值Δt；
（3）能打在挡板上的粒子占所有粒子的比率η．
【答案】（1）L=
（2）
（3）
【解析】
（1）由向心力公式得
qvB=m
解得
r=
因为OP=r，则水平向右出射的粒子运动轨迹恰好与挡板相切，运动轨迹如图甲所示，设此时打在挡板上的点为A，A点与P点间距离L=
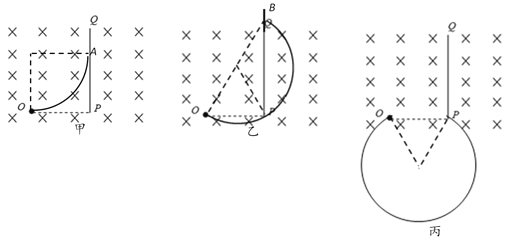
（2）粒子在磁场中运动周期
当粒子擦着最下端P点，打到挡板右侧最远处B点，轨迹如图乙所示，弧线圆心角
，
此时有最短运动时间
当粒子从右侧恰好打在P点时，轨迹如图丙所示，弧线圆心角
，
此时有最长运动时间
最长时间与最短时间的差值
Δt=t2－t1=
（3）图甲、图丙所示轨迹对应的出射方向之间的粒子都能打在板上，粒子出射速度方向能变化的角度为α=
，
打到板上的粒子占所有粒子的比率为
η=
=
练习册系列答案
相关题目
