Question

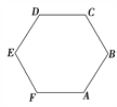
【题目】如图所示，倾角为θ、质量为M的斜面固定在水平面上，在斜面上固定半径为R的光滑半圆环，AB是半圆环的直径。现将质量为m的小球（可视为质点）紧贴着环的内侧，沿AD方向以初速度vo发射，小球可以沿环内侧运动至环的最高点。已知小球与斜面之间的动摩擦因数为μ，重力加速度为g。求

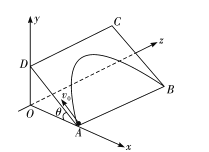
(1)斜面对小球的摩擦力所做的功Wf;

(2)vo至少为多少？

(3)解除固定后，斜面只能沿x轴方向无摩擦滑动，换一质量也为m的光滑小球，紧贴环的内侧，沿AD方向以速度V发射，当小球沿环内侧运动至环的最高点时，求斜面的速度V’的大小。

Answer 1

【答案】(1) (2) (3)

【解析】(1)如图a所示，

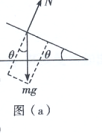
小球在斜面上运动时所受支持力

摩擦力

摩擦力所做的功

解得：；

(2)小球在圆环最高点E的速度为v，由动能定理

小球能运动到圆环最高点E，如图b所示，

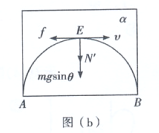
在E点受环的支持力

由圆周运动规律

解得：；

(3)斜面解除锁定，小球沿环内侧运动的过程中，小球和斜面组成的系统沿x轴方向动量守恒

解得：。