题目内容
11. 如图所示,装置的左边AB部分是长为L1=1m的水平面.一水平放置的轻质弹簧左端固定并处于原长状态;装置的中间BC部分是长为L2=2m的水平传送带,它与左右两边的台面等高,并能平滑对接,传送带始终以v=2m/s的速度顺时针转动;装置的右边是一光滑的曲面,质量m=1kg的小滑块从其上距水平台面h=1m的D处由静止释放,滑块向左最远到达O点,OA间距x=0.1m,并且弹簧始终处在弹性限度内.已知物块与传送带及左边水平面之间的摩擦因数μ=0.25,取g=10m/s2.
如图所示,装置的左边AB部分是长为L1=1m的水平面.一水平放置的轻质弹簧左端固定并处于原长状态;装置的中间BC部分是长为L2=2m的水平传送带,它与左右两边的台面等高,并能平滑对接,传送带始终以v=2m/s的速度顺时针转动;装置的右边是一光滑的曲面,质量m=1kg的小滑块从其上距水平台面h=1m的D处由静止释放,滑块向左最远到达O点,OA间距x=0.1m,并且弹簧始终处在弹性限度内.已知物块与传送带及左边水平面之间的摩擦因数μ=0.25,取g=10m/s2.(1)求弹簧获得的最大弹性势能?
(2)求滑块再次回到右边曲面部分所能到达的最大高度;
(3)若滑块质量m′=2kg,求滑块到达O点的速度.
分析 (1)滑块从D到O过程,其重力势能转化为内能和弹簧的弹性势能,由能量守恒定律求解弹簧储存的最大弹性势能;
(2)根据能量守恒定律求得滑块第二次经过B点时的速度大小,根据此速度与传送带速度的大小关系,判断出滑块将做匀加速运动,由运动学公式求出滑块的速度增加到与传送带相等时,通过的位移,即可知道滑块离开传送带时的速度.滑块从C到再次回到右边曲面部分所能到达的最大高度的过程中,重力做功,由动能定理求解最大高度.
(3)滑块到达O点时弹性势能不变,再由能量守恒求解滑块到达O点的速度.
解答 解:(1)滑块从D到O过程,由能量守恒定律得
EP=mgh-μmg(L1+L2-x)
解得,EP=2.75J
(2)设滑块再次到达B处的速度为v2,对滑块从O到再次到达B的过程,根据能量守恒得
EP=μmg(L1-x)+$\frac{1}{2}m{v}_{1}^{2}$,解得 v1=1m/s<v=2m/s
则知滑块再次滑上传送带后将匀加速运动,由牛顿第二定律得
μmg=ma,得a=2.5m/s2.
速度增加到与传送带相同所经历的位移为
L=$\frac{{v}^{2}-{v}_{1}^{2}}{2a}$=0.6m<L2=2m,
可知,滑块接着相对传送带静止,速度为v=2m/s
对从C到最高点的过程,由动能定理得
-mgh′=0-$\frac{1}{2}mv{′}^{2}$
解得,h′=0.2m
(3)若滑块质量m′=2kg,滑块从D到O过程,由能量守恒定律得
EP+μ•2mg(L1+L2-x)+$\frac{1}{2}•2m{v}_{O}^{2}$=2mgh
解得 vO≈2m/s
答:
(1)弹簧获得的最大弹性势能是2.75J.
(2)滑块再次回到右边曲面部分所能到达的最大高度是0.2m;
(3)若滑块质量m′=2kg,滑块到达O点的速度是2m/s.
点评 本题是多过程问题,分析滑块经历的过程,抓住各个过程的规律,运用能量守恒定律、牛顿第二定律和运动学公式结合按时间顺序分析和计算.

 在倾角为θ的固定光滑斜面上有两个用轻弹簧相连接的物块A、B,它们的质量分数为m1、m2,弹簧劲度系数为k,C为一固定挡板,系统处于静止状态.现用一平行于斜面向上的恒力F拉物块A使之向上运动,当物块B刚要离开挡板C时,物块A运动的距离为d,速度为v.则此时( )
在倾角为θ的固定光滑斜面上有两个用轻弹簧相连接的物块A、B,它们的质量分数为m1、m2,弹簧劲度系数为k,C为一固定挡板,系统处于静止状态.现用一平行于斜面向上的恒力F拉物块A使之向上运动,当物块B刚要离开挡板C时,物块A运动的距离为d,速度为v.则此时( )| A. | 拉力做功的瞬时功率为Fvsinθ | |
| B. | 物块B满足m2gsinθ<kd | |
| C. | 物块A的加速度为$\frac{F-kd}{{m}_{1}}$ | |
| D. | 弹簧弹性势能的增加量为Fd-m1gdsinθ-$\frac{1}{2}$m1v2 |
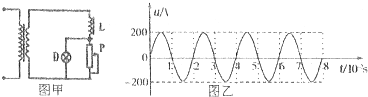
| A. | 图乙所示电压的瞬时值表达式为μ=200sin(100πt)V | |
| B. | 变压器副线圈两端的电压为220V | |
| C. | 若仅将变阻器的滑片P向下滑动,灯泡将变亮 | |
| D. | 若仅图乙中交变电压的周期变大,灯泡将变暗 |
 空间存在如图所示的电场,AB为同一电场线上的两点,现在AB间连接一根光滑曲管,且曲管与电场线重合,一质量为m的带电粒子以一定的初速度从A点运动到B点,重力不计,以下分析正确的是( )
空间存在如图所示的电场,AB为同一电场线上的两点,现在AB间连接一根光滑曲管,且曲管与电场线重合,一质量为m的带电粒子以一定的初速度从A点运动到B点,重力不计,以下分析正确的是( )| A. | 该粒子一定带正电 | |
| B. | 该粒子运动过程中机械能守恒 | |
| C. | 若某一瞬时带点粒子速度为v,对管压力为N,则所处位置曲率半径为$\frac{m{v}^{2}}{N}$ | |
| D. | 带电粒子运动过程中速度有可能先增大后减小 |
| A. | “神舟六号”的轨道高度比“神舟五号”略高 | |
| B. | “神舟六号”在轨道上运行的速度比“神舟五号”略小 | |
| C. | 飞船处于失重是因为地球对飞船的万有引力极小 | |
| D. | “神舟六号”运行时的向心加速度比“神舟五号”略小 |
| A. | 氡的半衰期为3.8天,4克氡原子核,经过7.6天就只剩下1克 | |
| B. | β衰变所释放的电子是原子核外的电子电离形成的 | |
| C. | 在α、β、γ这三种射线中,γ射线的穿透能力最强,α射线的电离能力最强 | |
| D. | 轴核(${\;}_{92}^{238}$U)衰变为铅核(${\;}_{82}^{206}$U)的过程中,要经过8次α衰变和10次β衰变 |
 如图所示,斜面的倾角为37°,在斜面底端正上方的O点将一小球以v0=3m/s的速度抛出,经过一段时间后落到斜面上时,其速度方向与斜面垂直,运动轨迹如图所示(g=10m/s2,sin37°=0.6,cos37°=0.8)求:抛出点O离斜面底端的高度.
如图所示,斜面的倾角为37°,在斜面底端正上方的O点将一小球以v0=3m/s的速度抛出,经过一段时间后落到斜面上时,其速度方向与斜面垂直,运动轨迹如图所示(g=10m/s2,sin37°=0.6,cos37°=0.8)求:抛出点O离斜面底端的高度.

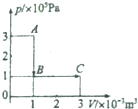 一定质量的理想气体从状态A变化到状态B,再变化到状态C,其状态变化过程的ρ-V图象如图所示,已知该气体在状态A时的温度为27℃,则:
一定质量的理想气体从状态A变化到状态B,再变化到状态C,其状态变化过程的ρ-V图象如图所示,已知该气体在状态A时的温度为27℃,则: