Question

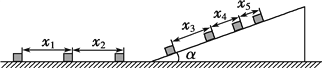
【题目】如图所示，上下表面均粗糙且足够长的木板A静置于水平地面上。物块B与A间的动摩擦因数为μ0＝0.2，物块C与A材料相同，与水平地面间的动摩擦因数均为μ＝0.1，物块B放在木板A上，它们的质量分别为mA＝3kg，mB＝1kg，mC＝2kg。开始时A、B、C均静止，A的右端与C左端相距L=4m。现对A施加一水平向右F＝6 N的恒力，A、B保持相对静止一起向右加速运动。一段时间后A与C正碰，且碰撞时间极短并粘在一起，最终A、B、C共速。取重力加速度g＝10 m/s2，求：

(1)A、C碰前瞬间B的速度大小？

(2)B相对A滑动的距离S

Answer 1

【答案】（1）2m/s；（2）0.133m

【解析】

(1)由题意可知，开始时，A和B相对静止一起向右运动，由动能定理得：

[F－μ(mA＋mB)g]L＝(mA＋mB)

解得A、C碰前瞬间B的速度大小

v1＝2m/s

(2)当A、C发生碰撞时，碰撞时间极短，A、C系统的动量守恒，则有

mAv1＝(mA＋mC)v2

解得

v2＝1.2m/s

A、C所受地面的摩擦力

Ff＝μ(mA＋mB＋mC)g＝6N＝F

所以A、B、C所受的合外力为零，系统的动量守恒，最终A、B、C共速，由动量守恒定律和能量守恒得

mBv1＋(mA＋mC)v2＝(mA＋mB＋mC)v3

mB＋(mA＋mC)＝(mA＋mB＋mC)＋μmBgS

解得

S=0.133m