��Ŀ����
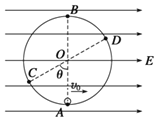
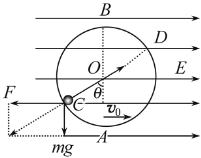
����Ŀ����ͼ��ʾ������ֱƽ���ڹ̶���Բ�ξ�Ե�����Բ����O�㣬�뾶Ϊr���ڱڹ⻬��A��B����ֱ���Բ������͵����ߵ㡣��������ڷ���ˮƽ���ҵ���ǿ�糡��һ����Ϊm���������С���ڹ���ڲ���������Բ���˶�![]() ���������
���������![]() ����C��ʱ�ٶ����O��C��������ֱ����ļн�
����C��ʱ�ٶ����O��C��������ֱ����ļн�![]() ���������ٶ�Ϊg��
���������ٶ�Ϊg��
![]() ��С�����ܵ��ĵ糡����С��
��С�����ܵ��ĵ糡����С��
![]() ��ǡ������������Բ���˶������D����ٶȣ�
��ǡ������������Բ���˶������D����ٶȣ�
![]() С����A���ٶ�
С����A���ٶ�![]() ���ʱ��С��B��ʱ�Թ����ѹ����С��
���ʱ��С��B��ʱ�Թ����ѹ����С��
���𰸡���![]() ��
��![]() ��
��![]()
��������
�⣺![]() ��֪����С���ڹ⻬����ֱԲ�������������Բ���˶�����C��ʱ�ٶ������ˣ�C������ֱƽ����Բ���˶�����������͵㡱��Ҳ����С����C��糡���������ĺ�������Բ�ĵķ�����ͼ��
��֪����С���ڹ⻬����ֱԲ�������������Բ���˶�����C��ʱ�ٶ������ˣ�C������ֱƽ����Բ���˶�����������͵㡱��Ҳ����С����C��糡���������ĺ�������Բ�ĵķ�����ͼ��
����![]()
��˵糡��Ϊ��![]()
![]() ����ֱƽ����Բ���˶�����������ߵ㡱��ǡ������������Բ���˶����ڡ���ߵ㡱����С�ٶȣ���
����ֱƽ����Բ���˶�����������ߵ㡱��ǡ������������Բ���˶����ڡ���ߵ㡱����С�ٶȣ���![]()
��ã�![]()
![]() ҪС��B��ʱ�Թ����ѹ����С��������С�ٶȾ���D�㣬������֪��D���ٶ���
ҪС��B��ʱ�Թ����ѹ����С��������С�ٶȾ���D�㣬������֪��D���ٶ���![]()
С���A��D�Ĺ����У��ɶ��ܶ����ã�![]()
������ã�![]()

��ϰ��ϵ�д�
�����Ŀ