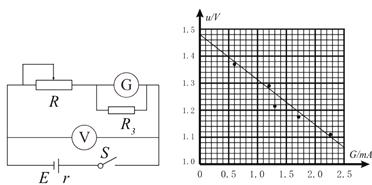
题目内容
【题目】在物理学中,常常用等效替代、类比、微小量放大等方法来研究问题,如在牛顿发现万有引力定律一百多年后,卡文迪许利用微小量放大法由实验测出了万有引力常量G的数值,如图所示是卡文迪许扭秤实验示意图。卡文迪许的实验常被称为是“称量地球质量”的实验,因为由G的数值及其他已知量,就可计算出地球的质量,卡文迪许也因此被誉为第一个称量地球的人。
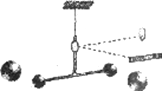
(1)若在某次实验中,卡文迪许测出质量分别为m1、m2相距为r的两个小球之间引力的大小为F,求万有引力常量G;
(2)若已知地球半径为R,地球表面重力加速度为g,万有引力常量为G,忽略地球自转的影响,请推导出地球质量M;
(3)取万有引力常量G=6.67×10-11N·m2/kg2,地球质量M=6.0×1024kg,月球质量m=7.3×1022kg,月地距离r=3.8×105km,计算月球和地球之间的万有引力大小。(结果保留一位有效数字)
【答案】(1) ![]() ; (2)M =gR2/G; (3)2×1020N
; (2)M =gR2/G; (3)2×1020N
【解析】
(1)根据万有引力定律有:F=![]()
解得:G=![]()
(2)设地球质量为M,在地球表面任一物体质量为m,在地球表面附近满足:![]()
得地球的质量为:M=![]()
(3)根据万有引力定律有:F=![]() =
=![]() N=2×1020kg,
N=2×1020kg,

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目