题目内容
如图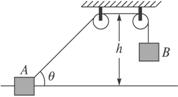
图
解析:物体A受到细线的拉力方向一直在变化,所以物体A受到的力是变力,很难用牛顿运动定律和运动学公式求解.但由于物体A和B以及地球组成的系统内只有重力做功,所以系统的机械能守恒.在物体A被拉至左侧定滑轮的正下方之前,细线的拉力使其加速;在物体A被拉至左侧定滑轮的正下方之后,细线的拉力使其减速.可见,物体A被拉至左侧定滑轮的正下方时,其速度最大.
物体A被拉至左侧定滑轮的正下方时获得最大速度,此时物体B的瞬时速度为0.以物体A所在水平面为参考平面,在从物体A刚被释放到物体A运动至左侧定滑轮正下方的过程中,对系统应用机械能守恒定律,有
![]() mv2=mg(
mv2=mg(![]() -h)
-h)
解得A所能获得的最大速度为:
v=![]() m/s=
m/s=

练习册系列答案
相关题目