题目内容
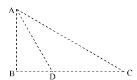
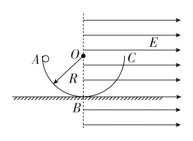
【题目】如图所示，光滑绝缘的半圆形轨道ABC固定在竖直面内，圆心为O，轨道半径为R，B为轨道最低点。该装置右侧的
圆弧置于水平向右的足够大的匀强电场中。某一时刻一个带电小球从A点由静止开始运动，到达B点时，小球的动能为E0，进入电场后继续沿轨道运动，到达C点时小球的电势能减少量为2E0，试求：
（1）小球所受重力和电场力的大小；
（2）小球脱离轨道后到达最高点时的动能。
【答案】（1）
（2）8E0
【解析】
(1)设带电小球的质量为m，则从A到B根据动能定理有：
mgR＝E0
则小球受到的重力为：
mg＝
方向竖直向下；
由题可知：到达C点时小球的电势能减少量为2E0，根据功能关系可知：
EqR＝2E0
则小球受到的电场力为：
Eq＝
方向水平向右，小球带正电。
(2)设小球到达C点时速度为vC，则从A到C根据动能定理有：
EqR＝
＝2E0
则C点速度为：
vC＝
方向竖直向上。
从C点飞出后，在竖直方向只受重力作用，做匀减速运动到达最高点的时间为：
在水平方向只受电场力作用，做匀加速运动，到达最高点时其速度为：
则在最高点的动能为：
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
