题目内容
【题目】天文学家将相距较近、仅在彼此的引力作用下运行的两颗恒星称为双星.双星系统在银河系中很普遍.利用双星系统中两颗恒星的运动特征可推算出它们的总质量.已知某双星系统中两颗恒星围绕它们连线上的某一固定点分别做匀速圆周运动,周期均为T,两颗恒星之间的距离为r.
(1)试推算这个双星系统的总质量.
(2)为研究此双星系统,发射微型飞行器A和B分别绕恒星A和B运动,成为恒星的卫星.已知A贴近A的表面做匀速圆周运动的周期为T1,A的半径为R1; B距B表面的高度为h,测得在该处做圆周运动的周期为T2,B的半径为R2.分别写出A和B的密度表达式.(万有引力常量为G)
【答案】(1)![]() (2)
(2)![]() ,
, 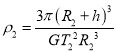
【解析】(1)设恒星A质量为M1,恒星B的质量为M2,做圆周运动的半径分别为r1、r2,根据题意有![]()
![]()
根据万有引力定律和牛顿定律,有![]()
![]()
联立解得![]()
(2)设微型飞行器A的质量为m1,恒星A质量为M1,A贴近天体表面运动时有
![]() ,
, ![]()
据数学知识可知天体的体积为: ![]()
故该恒星A的密度: ![]()
设微型飞行器B的质量为m2,恒星B的质量为M2,B距天体表面距离为h时,
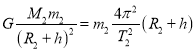 ,
,
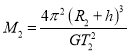
据数学知识可知天体的体积为: ![]()


练习册系列答案
相关题目