题目内容
【题目】一质量m=0.5 kg的滑块以一定的初速度冲上一倾角θ=37°足够长的斜面,某同学利用传感器测出了滑块冲上斜面过程中多个时刻的瞬时速度,并用计算机做出了小物块上滑过程的v-t图象,如图所示.(最大静摩擦力等于滑动摩擦力,取sin37°=0.6,cos37°=0.8,g="10" m/s2)求:
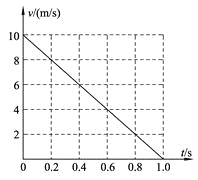
(1)滑块与斜面间的动摩擦因数
(2)判断滑块最后能否返回斜面底端?若能返回,求出返回 斜面底端时的速度大小;若不能返回,求出滑块停在什么位置.
【答案】(1)μ=0. 5(2)![]()
【解析】
(1) 由图象可知,滑块的加速度a=![]() =
=![]() m/s2="10" m/s2
m/s2="10" m/s2
滑块冲上斜面过程中根据牛顿第二定律,有mgsinθ+μmgcosθ=ma
代入数据解得μ=0.5
(2) 滑块速度减小到零时,重力的下滑分力大于最大静摩擦力,能再下滑
由匀变速直线运动的规律,滑块向上运动的位移s=![]() ="5" m
="5" m
滑块下滑过程中根据牛顿第二定律,有mgsinθ-μmgcosθ=ma2,a2="2" m/s2
由匀变速直线运动的规律,滑块返回底端的速度v=![]() =
=![]() m/s
m/s
本题考查速度速度时间图像和牛顿第二定律的应用,由图像的斜率可求得加速度大小,再由牛顿第二定律列式可求得动摩擦因数大小,由匀变速直线运动公式可求得上升的最大距离,下滑过程中由重力沿斜面向下的分力和滑动摩擦力提供加速度,再由位移与速度的关系求得末速度大小

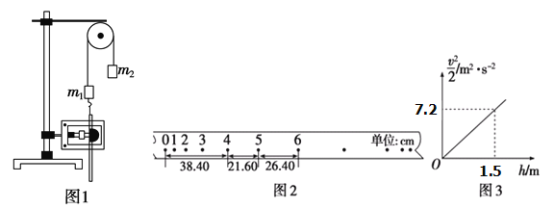
【题目】某同学用图甲装置完成“探究小车速度随时间变化规律”实验,打点计时器接在频率为50Hz的交流电源上。图乙是实验中该同学得到的一条清晰纸带,纸带上各相邻计数点间还有4个计时点未画出。数据处理时,该同学将计数点0作为计时开始的点,测出其余各点到0点的距离x,记录在下表中。

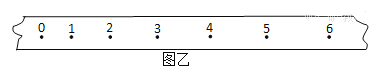
计数点 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
t/s | 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 |
x/cm | 0 | 1.40 | 3.30 | 5.70 | 8.60 | 12.00 | 15.90 |
(1)打点计时器打下点4时小车的瞬时速度v4=________m/s。(结果保留3位有效数字)
(2)小车的加速度为a =________ m/s2。(结果保留2位有效数字)