Question

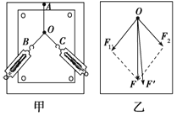
【题目】如图所示，将两根劲度系数均为k、原长均为L的轻弹簧，一端固定于水平天花板上相距为2L的两点，另一端共同连接一质量为m的物体，平衡时弹簧与竖直方向的夹角为37°.若将物体的质量变为M，平衡时弹簧与竖直方向的夹角为53°(sin37°＝0.6，cos37°＝0.8)，M：m等于(　　)

A.9:32B.9:16C.3:8D.3:4

Answer 1

【答案】A

【解析】

由几何知识得左图中弹簧的伸长量为：

右图中弹簧的伸长量为：

根据胡克定律：F=kx，k相同，则得两情况下弹簧拉力之比为：

F1：F2=x1：x2=8：3

根据平衡条件得：
左图中有

2F1cos37°=mg

右图中有

2F2cos53°=Mg

联立得：

A．9:32，与结论相符，选项A正确；

B．9:16，与结论不相符，选项B错误；

C．3:8，与结论不相符，选项C错误；

D．3:4，与结论不相符，选项D错误；

故选A。