题目内容
6. 如图甲所示,水平面有一小滑块静止在A点,滑块质量m=2kg.水平面与一足够长的斜面通过一小段光滑圆弧连接,斜面倾角θ=30°.已知滑块与水平面间的动摩擦因数μ=0.2,某时刻给滑块施加一水平恒力F,滑块运动2s后第一次达到斜面底端B点,同时撤掉水平力F.滑块在AB间运动的位移和时间平方的关系如图乙所示,最后滑块回到A点静止,g=10m/s2.求:
如图甲所示,水平面有一小滑块静止在A点,滑块质量m=2kg.水平面与一足够长的斜面通过一小段光滑圆弧连接,斜面倾角θ=30°.已知滑块与水平面间的动摩擦因数μ=0.2,某时刻给滑块施加一水平恒力F,滑块运动2s后第一次达到斜面底端B点,同时撤掉水平力F.滑块在AB间运动的位移和时间平方的关系如图乙所示,最后滑块回到A点静止,g=10m/s2.求:(1)水平恒力F的大小;
(2)滑块运动的时间.
分析 (1)根据乙图求得加速度,根据牛顿第二定律求得拉力;
(2)根据运动学公式求得到达B点的速度,由于滑块从A到B和B到A是对称的,滑块返回到B点速度相同,判断蹙额斜面光滑,利用牛顿第二定和运动学公式即可求得运动的总时间
解答 解:(1)由图乙可知滑块在水平面上做匀加速直线运动,图线斜率$k=\frac{1}{2}{a}_{1}$ 得 ${a}_{1}=2m/{s}^{2}$
根据牛顿第二定律得:F-μmg=ma1
解得F=8 N
(2)滑块在B点:v=a1t1=4m/st1=2s
滑块从B点到A点:μmg=ma2
得 ${a}_{2}=2m/{s}^{2}$
由此可知滑块从A到B和B到A是对称的,滑块返回到B点速度也是 v=a2t2=4m/s
由B到A的时间 t2=2s
再由对称性可知,滑块在斜面上运动也是对称的,即在斜面上滑块先作匀减速运动到速度为零,然后做匀加速运动,滑块向上和向下运动的加速度相同,滑块不受摩擦力,故斜面是光滑的
故在斜面上有 mgsinθ=ma3
由 v=a3t3=4m/s 得 t3=0.8s
滑块运动的时间 t=t1+t2+t3=5.6s
答:(1)水平恒力F的大小为8N;
(2)滑块运动的时间为5.6s.
点评 本题是牛顿第二定律和运动学的综合应用,关键要抓住物体在斜面上运动具有对称性,上滑和下滑时间相等,不能漏解.

练习册系列答案
相关题目
4. 电动汽车后备箱盖,一般都配有可伸缩的液压杆,如图1所示,其示意图如图2所示,可伸缩液压杆上端固定于后盖上A点,下端固定于箱内O′点,B也为后盖上一点,后盖可绕过O点的固定铰链转动,在合上后备箱盖的过程中( )
电动汽车后备箱盖,一般都配有可伸缩的液压杆,如图1所示,其示意图如图2所示,可伸缩液压杆上端固定于后盖上A点,下端固定于箱内O′点,B也为后盖上一点,后盖可绕过O点的固定铰链转动,在合上后备箱盖的过程中( )
 电动汽车后备箱盖,一般都配有可伸缩的液压杆,如图1所示,其示意图如图2所示,可伸缩液压杆上端固定于后盖上A点,下端固定于箱内O′点,B也为后盖上一点,后盖可绕过O点的固定铰链转动,在合上后备箱盖的过程中( )
电动汽车后备箱盖,一般都配有可伸缩的液压杆,如图1所示,其示意图如图2所示,可伸缩液压杆上端固定于后盖上A点,下端固定于箱内O′点,B也为后盖上一点,后盖可绕过O点的固定铰链转动,在合上后备箱盖的过程中( )| A. | A点相对O′点做圆周运动 | |
| B. | A与B相对于O点转动的线速度大小相同 | |
| C. | A与B相对于O点转动的角速度大小相同 | |
| D. | A与B相对于O点转动的向心加速度大小相同 |
5.某实验小组利用如图甲所示的电路测定电源的电动势和内阻,提供的器材为:
A.干电池两节,每节电池的电动势为1.5V,内阻未知
B.直流电压表V1、V2,内阻很大
C.直流电流表A,内阻可忽略不计
D.定值电阻R0,阻值未知,但不小于5Ω?
E.滑动变阻器
F.导线和开关

(1)该同学设计了如图甲所示的电路,请你用画线做导线正确连接图乙所示的实物图.
(2)该同学利用图乙电路完成实验时,由于某跟导线发生断路故障,因此只记录了一个电压表和电流表的示数,如表所示:
试利用表格中的数据作出U-I图.由图象可知,两节干电池总电动势值为2.88V,总内阻为3.37(结果保留三位有效数字).由计算得到的数据可以判断能够正确示数的电压表应为表V1(选填“V1”或“V2”).
A.干电池两节,每节电池的电动势为1.5V,内阻未知
B.直流电压表V1、V2,内阻很大
C.直流电流表A,内阻可忽略不计
D.定值电阻R0,阻值未知,但不小于5Ω?
E.滑动变阻器
F.导线和开关

(1)该同学设计了如图甲所示的电路,请你用画线做导线正确连接图乙所示的实物图.
(2)该同学利用图乙电路完成实验时,由于某跟导线发生断路故障,因此只记录了一个电压表和电流表的示数,如表所示:
| U/V | 2.62 | 2.48 | 2.34 | 2.20 | 2.06 | 1.92 |
| I/A | 0.08 | 0.12 | 0.19 | 0.20 | 0.24 | 0.28 |
2. 氢原子能级的示意图如图所示,大量氢原子从n=4的能级向n=2的能级跃迁时辐射出可见光a,从n=3的能级向n=2的能级跃迁时辐射出可见光b,则( )
氢原子能级的示意图如图所示,大量氢原子从n=4的能级向n=2的能级跃迁时辐射出可见光a,从n=3的能级向n=2的能级跃迁时辐射出可见光b,则( )
 氢原子能级的示意图如图所示,大量氢原子从n=4的能级向n=2的能级跃迁时辐射出可见光a,从n=3的能级向n=2的能级跃迁时辐射出可见光b,则( )
氢原子能级的示意图如图所示,大量氢原子从n=4的能级向n=2的能级跃迁时辐射出可见光a,从n=3的能级向n=2的能级跃迁时辐射出可见光b,则( )| A. | 在水中传播时,a光较b光的速度小 | |
| B. | 氢原子从n=4的能级向n=3的能级跃迁时辐射出的光子的能量可能小于0.66eV | |
| C. | 一群处于n=4能级上的氢原子向低能级跃迁时最多产生3种谱线 | |
| D. | 若a光照射某种金属能发生光电效应,则b光照射这种金属也一定能发生光电效应 |
1.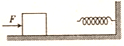 如图所示,一木块在光滑水平面上受一恒力F作用,前方固定一足够长的水平轻弹簧,则当木块接触弹簧后,下列判断正确的是( )
如图所示,一木块在光滑水平面上受一恒力F作用,前方固定一足够长的水平轻弹簧,则当木块接触弹簧后,下列判断正确的是( )
 如图所示,一木块在光滑水平面上受一恒力F作用,前方固定一足够长的水平轻弹簧,则当木块接触弹簧后,下列判断正确的是( )
如图所示,一木块在光滑水平面上受一恒力F作用,前方固定一足够长的水平轻弹簧,则当木块接触弹簧后,下列判断正确的是( )| A. | 木块立即做减速运动 | |
| B. | 木块在一段时间内速度仍增大 | |
| C. | 当F等于弹簧弹力时,木块速度最大 | |
| D. | 弹簧压缩量最大时,木块速度为零但加速度不为零 |
11.如图甲所示,水平地面上静止放置一质量为M的木板,木板的左端有一个可视为质点的、质量为m=1kg的滑块.现给滑块一向右的初速度v0=10m/s,此后滑块和木板在水平面上运动的速度图象如图乙所示,滑块最终刚好停在木板的右端,取g=10m/s2.下列说法正确的是( )

| A. | 滑块与木板间的动摩擦因数为μ1=0.4 | |
| B. | 木板与地面间的动摩擦因数为μ2=0.1 | |
| C. | 木板的长度为L=4m | |
| D. | 木板的质量为M=1.5kg |
18. 身体素质拓展训练中,人从竖直墙壁的顶点A沿光滑杆自由下滑倾斜的木板上(人可看做质点),若木板的倾斜角不同,人沿着三条不同路径AB、AC、AD滑到木板上的时间分别为t1、t2、t3,若已知AB、AC、AD与板的夹角分别为70°、90°和105°,则 ( )
身体素质拓展训练中,人从竖直墙壁的顶点A沿光滑杆自由下滑倾斜的木板上(人可看做质点),若木板的倾斜角不同,人沿着三条不同路径AB、AC、AD滑到木板上的时间分别为t1、t2、t3,若已知AB、AC、AD与板的夹角分别为70°、90°和105°,则 ( )
 身体素质拓展训练中,人从竖直墙壁的顶点A沿光滑杆自由下滑倾斜的木板上(人可看做质点),若木板的倾斜角不同,人沿着三条不同路径AB、AC、AD滑到木板上的时间分别为t1、t2、t3,若已知AB、AC、AD与板的夹角分别为70°、90°和105°,则 ( )
身体素质拓展训练中,人从竖直墙壁的顶点A沿光滑杆自由下滑倾斜的木板上(人可看做质点),若木板的倾斜角不同,人沿着三条不同路径AB、AC、AD滑到木板上的时间分别为t1、t2、t3,若已知AB、AC、AD与板的夹角分别为70°、90°和105°,则 ( )| A. | t1>t2>t3 | B. | t1<t2<t3 | ||
| C. | t1=t2=t3 | D. | 不能确定t1、t2、t3之间的关系 |
15.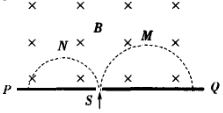 如图所示,PQ板的上方存在匀强磁场,质量和电荷量都相等的带电粒子M和N,以不同的速率经小孔S垂直PQ板进入匀强磁场,运行的半圆轨迹如图中虚线所示.下列表述正确的是( )
如图所示,PQ板的上方存在匀强磁场,质量和电荷量都相等的带电粒子M和N,以不同的速率经小孔S垂直PQ板进入匀强磁场,运行的半圆轨迹如图中虚线所示.下列表述正确的是( )
 如图所示,PQ板的上方存在匀强磁场,质量和电荷量都相等的带电粒子M和N,以不同的速率经小孔S垂直PQ板进入匀强磁场,运行的半圆轨迹如图中虚线所示.下列表述正确的是( )
如图所示,PQ板的上方存在匀强磁场,质量和电荷量都相等的带电粒子M和N,以不同的速率经小孔S垂直PQ板进入匀强磁场,运行的半圆轨迹如图中虚线所示.下列表述正确的是( )| A. | M带负电,N带正电 | B. | M的速率大于N的速率 | ||
| C. | 洛伦兹力对M、N做正功 | D. | M的运行时间大于N的运行时间 |
16.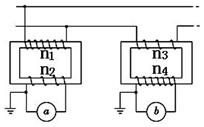 如图所示,在某一输电线路的起始端接入两个理想变压器,原、副线圈的匝数比分别 为 n1:n2=100:1 和 n3:n4=1:100,图中 a、b 表示电流表或电压表,已知电压表的示数为 22V,电流表的示数为 1A,则以下说法正确的是( )
如图所示,在某一输电线路的起始端接入两个理想变压器,原、副线圈的匝数比分别 为 n1:n2=100:1 和 n3:n4=1:100,图中 a、b 表示电流表或电压表,已知电压表的示数为 22V,电流表的示数为 1A,则以下说法正确的是( )
 如图所示,在某一输电线路的起始端接入两个理想变压器,原、副线圈的匝数比分别 为 n1:n2=100:1 和 n3:n4=1:100,图中 a、b 表示电流表或电压表,已知电压表的示数为 22V,电流表的示数为 1A,则以下说法正确的是( )
如图所示,在某一输电线路的起始端接入两个理想变压器,原、副线圈的匝数比分别 为 n1:n2=100:1 和 n3:n4=1:100,图中 a、b 表示电流表或电压表,已知电压表的示数为 22V,电流表的示数为 1A,则以下说法正确的是( )| A. | a 为电流表,b 为电压表 | B. | a 为电压表,b 为电流表 | ||
| C. | 输电线路总电阻为 22Ω | D. | 线路输送电功率是 220 kW |