��Ŀ����
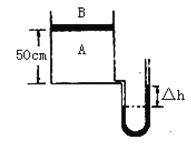
����Ŀ����ͼ����ʾ�������㹻�������費�Ƶ�ƽ�н���������� L��1m������ƽ ����ˮƽ��ļн�����37�����¶�������ֵ R��1���ĵ��裻���� m��1kg����ֵ r
��1�������ʽ����� cd �����������ϣ����������¶˵ľ��� L1��1m�����뵼�� ��ֱ���������ýӴ����뵼���Ķ�Ħ����������0.9������װ�ô����뵼��ƽ�� ��ֱ������Ϊ��������ǿ�ų������Ÿ�Ӧǿ����ʱ��仯�������ͼ����ʾ���� Ϊ���Ħ�������ڻ���Ħ��������֪�� 0��1.0s �ڣ������� cd ���־�ֹ��ȡ sin37����0.6��cos37����0.8��g��10m��s2��

��1���� 0��1.0s ��ͨ�������� cd �ĵ������
��2���� t��1.1s ʱ�̣������� cd ����Ħ�����Ĵ�С�ͷ���
��3��1.2s �����Խ����� cd ʩ��һ��б�����ϵ����� F��ʹ������ cd ��б������ �����ٶȴ�С![]() ���ȼ����˶�����д������ F ��ʱ�� t������ʩ�� F ʱ�� ʼ��ʱ���仯�Ĺ�ϵʽ��
���ȼ����˶�����д������ F ��ʱ�� t������ʩ�� F ʱ�� ʼ��ʱ���仯�Ĺ�ϵʽ��
���𰸡���1��![]() ��2��
��2��![]() �����ص������ϣ�3��
�����ص������ϣ�3��![]()
��������(1)��01.0s�ڣ�������cd�ϲ����ĸ�Ӧ�綯��Ϊ��
E=![]()
����S=L1��L=1��1=1m��
�ɱպϵ�·ŷķ�����У�
I=![]()
������01.0s�ڻ�·�е����㶨���ʵ���q=It
����t=1s��
������ã�q=1C��
(2)��01.1s�ڽ�����cd���־�ֹ,����01.1s�ڻ�·�еĵ�������,t=1.1sʱ,������cd���ܰ�����F��=B1IL=0.2��1��1=0.2N�������ص������£�
�ֵ���Խ�����cd�����Ħ����f��=��mgcos37=0.9��10��0.8=7.2N��
����mgsin37+F��=6.2N<f�䣬��֪����������������Ա��־�ֹ
������Ħ����Ϊf=mgsin37+F��=6.2N�������ص������ϣ�
(2)1.2s�������cd�ϲ����ĸ�Ӧ�綯��ΪE��=B2Lv������v=at��
������cd���ܰ������Ĵ�СΪ��
F��=B2I2L,����I2=![]()
��ţ�ٵڶ������У�
Fmgsin����mgcos��F��=ma
��ã�F=15.2+0.16t��(N)