题目内容
6.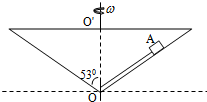 如图所示,V形转盘可绕竖直中心轴OO'转动,V形转盘的侧面与竖直转轴间的夹角均为α=53°.盘上放着质量为1kg的物块A,物块A用长为1m的细线系于转盘中心的O处,细线能承受的最大拉力为8N,A与转盘间的动摩擦因数μ为0.5,且可认为最大静摩擦力等于滑动摩擦力,在物块A与转盘一起转动的过程中,细线始终处于伸直状态.
如图所示,V形转盘可绕竖直中心轴OO'转动,V形转盘的侧面与竖直转轴间的夹角均为α=53°.盘上放着质量为1kg的物块A,物块A用长为1m的细线系于转盘中心的O处,细线能承受的最大拉力为8N,A与转盘间的动摩擦因数μ为0.5,且可认为最大静摩擦力等于滑动摩擦力,在物块A与转盘一起转动的过程中,细线始终处于伸直状态.(1)当物块A随转盘一起做匀速转动,且其所受的摩擦力为零时,转盘转动的角速度多大(结果可以保留根式);
(2)为保证细线一直处于伸直状态,物块A跟随转盘一起匀速转动的角速度的范围(g取10m/s2).
分析 (1)当物块A随转盘做匀速转动所受的摩擦力为零时,此时绳处于松弛状态,由支持力和重力的合力提供向心力,竖直方向由平衡条件列式,水平方向根据牛顿第二定律列式即可求解;
(2)当物块A所受摩擦力沿斜面向上,且等于最大静摩擦力时,物块转动的角速度最小.当物块A所受摩擦力沿斜面向下,且等于最大静摩擦力,绳子拉力达到最大值时,物块转动的角速度最大.竖直方向由平衡条件列式,水平方向根据牛顿第二定律列式即可求解角速度的最小值和最大值,即可得到角速度的范围.
解答 解:(1)当摩擦力为零时,物块只受重力和支持力,由题意,由牛顿第二定律可得:
${F_N}cos{37^o}=mg$…①
${F_N}sin{37^o}=m{ω^2}r$…②
又 r=lcos37°…③
所以:$ω=\frac{{5\sqrt{6}}}{4}rad/s$
(2)当物块A所受摩擦力沿斜面向上,且等于最大静摩擦力时,物块转动的角速度最小
由受力分析可得:
${F_N}sin{37^o}-fcos{37^o}=mω_1^2r$…④
${F_N}cos{37^o}+fsin{37^o}=mg$…⑤
又 f=μFN …⑥
联立③④⑤⑥可得:${ω_1}=\sqrt{\frac{g}{{lcos{{37}^o}}}•\frac{{sin{{37}^o}-μcos{{37}^o}}}{{cos{{37}^o}+μsin{{37}^o}}}}=\frac{{5\sqrt{11}}}{11}$rad/s
当物块A所受摩擦力沿斜面向下,且等于最大静摩擦力,绳子拉力达到最大值时,物块转动的角速度最大
由受力分析可知:
${F_N}sin{37^o}+fcos{37^o}+Tcos{37^o}=mω_2^2r$…⑦
${F_N}cos{37^o}=mg+fsin{37^o}+Tsin{37^o}$…⑧
联立③⑥⑦⑧可得:${ω_2}=\sqrt{\frac{{mg+Tsin{{37}^o}}}{{mlcos{{37}^o}}}•\frac{{sin{{37}^o}+μcos{{37}^o}}}{{cos{{37}^o}-μsin{{37}^o}}}+\frac{T}{ml}}=3\sqrt{5}$rad/s
所以:$\frac{5\sqrt{11}}{11}$ rad/s≤ω≤$3\sqrt{5}$ rad/s
答:(1)转盘转动的角速度是$\frac{5\sqrt{6}}{4}$rad/s.
(2)物块A跟随转盘一起匀速转动的角速度的范围为:$\frac{5\sqrt{11}}{11}$ rad/s≤ω≤$3\sqrt{5}$ rad/s.
点评 本题的关键是能对物块进行受力分析,根据竖直方向由平衡条件列式及水平方向牛顿第二定律列式,并能根据最大静摩擦力的表达式分析.

| A. | 月球绕地球运动的向心加速度a=$\frac{4{π}^{2}}{{T}^{2}}$R | |
| B. | 月球的质量M=$\frac{{v}_{0}^{2}{R}^{2}}{2Gh}$ | |
| C. | 月球的第一宇宙速度v1=v0$\sqrt{\frac{R}{2h}}$ | |
| D. | 月球同步卫星的高度h0=$\root{3}{\frac{{v}_{0}^{2}{R}^{2}{T}^{2}}{8{π}^{2}h}}$ |
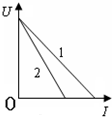 如图为两个电源的U-I图象,其中U为闭合电路的路端电压,I为电路中的干路电流,下列判断错误的是( )
如图为两个电源的U-I图象,其中U为闭合电路的路端电压,I为电路中的干路电流,下列判断错误的是( )| A. | 电动势E1=E2,发生短路时的电流 I1>I2 | |
| B. | 电动势E1=E2,内阻 r2>r1 | |
| C. | 电动势E1>E2,内阻r1<r2 | |
| D. | 当两电源的工作电流变化量相同时,电源2的路端电压变化大 |
 如图所示,一足够长的固定光滑斜面与水平面的夹角为53°,物体A以初速度v1从斜面顶端水平抛出,物体B在斜面上距顶端L=20m处同时以速度v2沿斜面向下匀加速运动,为使物体A和物体B在斜面上经历时间t相遇,则下列各组速度和时间中满足条件的是(cos53°=0.6,sin53°=0.8,g=l0m/s2)( )
如图所示,一足够长的固定光滑斜面与水平面的夹角为53°,物体A以初速度v1从斜面顶端水平抛出,物体B在斜面上距顶端L=20m处同时以速度v2沿斜面向下匀加速运动,为使物体A和物体B在斜面上经历时间t相遇,则下列各组速度和时间中满足条件的是(cos53°=0.6,sin53°=0.8,g=l0m/s2)( )| A. | v1=18m/s,v2=6m/s,t=3s | B. | v1=15m/s,v2=6m/s,t=3s | ||
| C. | v1=18m/s,v2=4m/s,t=4s | D. | v1=15m/s,v2=4m/s,t=4s |
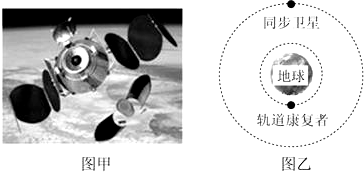
| A. | 在图示轨道上,“轨道康复者”的速度小于7.9km/s | |
| B. | 在图示轨道上,“轨道康复者”的加速度大小是地球同步卫星的16倍 | |
| C. | 在图示轨道上,“轨道康复者”的周期为4h | |
| D. | 若要对该同步卫星实施拯救,“轨道康复者”应从图示轨道上加速,然后与同步卫星对接 |
| A. | 由E=$\frac{F}{q}$知,若q减小为原来的$\frac{1}{2}$,则该处电场强度变为原来的2倍 | |
| B. | 由E=k$\frac{Q}{{r}^{2}}$知,E与Q成正比,而与r2成反比 | |
| C. | 由E=k$\frac{Q}{{r}^{2}}$知,在以Q为球心、r为半径的球面上,各处电场强度均相同 | |
| D. | 电场中某点电场强度方向就是该点所放电荷受到的电场力的方向 |
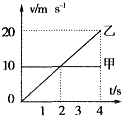
| A. | 乙的加速度为4m/s2 | B. | 在4s末甲、乙相距最远 | ||
| C. | 在2s末甲乙相遇 | D. | 前4s内甲乙平均速度相等 |