题目内容
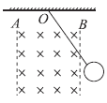
【题目】如图所示，竖直平面内放置相距为L的两条足够长的光滑平行金属导轨，上端接有阻值为R的定值电阻，磁感应强度为B的匀强磁场垂直于导轨平面。将质量为m的导体棒AC由静止释放，导体棒始终与导轨垂直且接触良好，不计导轨和导体棒的电阻，重力加速度为g，则在导体棒运动到稳定的过程中（ ）
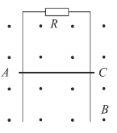
A.导体棒先做加速运动，然后做减速运动
B.导体棒中的电流方向为由A指向C
C.导体棒运动的最大速度
D.电阻产生的焦耳热等于导体棒重力势能的减少量
【答案】C
【解析】
AC．据牛顿第二定律可得金属棒下滑过程中的加速度为
由此可知，速度增大，加速度减小，所以导体棒达到稳定状态前做加速度减少的加速运动．
当加速度为0时，导体棒运动的速度最大，所以导体棒运动的最大速度为
故C正确，A错误；
B．根据右手定则可知，导体棒中的电流方向为由C指向A，故B错误；
D．根据能量守恒定律可知，导体棒重力势能的减少量等于电阻产生的焦耳热和导体棒的动能之和，故D错误；
故选C。
阅读快车系列答案
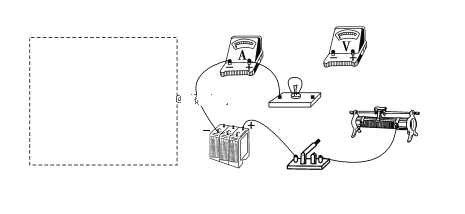
【题目】利用如图（a）所示电路，可以测量电源的电动势和内阻，所用的实验器材有：待测电源，电阻箱R（最大阻值999.9Ω），电阻R0（阻值为3.0Ω），电阻R1（阻值为3.0Ω），电流表A（量程为200mA，内阻为RA=6.0Ω），开关S。
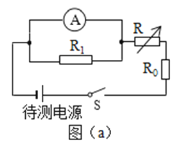
实验步骤如下：
①将电阻箱阻值调到最大，闭合开关S；
②多次调节电阻箱，记下电流表的示数I和电阻箱相应的阻值R
③以
为纵坐标，R为横坐标，作—R图线（用直线拟合）；
④求出直线的斜率k，在纵坐标轴上的截距b
回答下列问题：
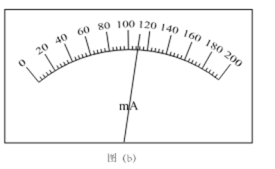
(1)实验得到的部分数据如下表所示，其中电阻R=3.0Ω时电流表的示数如图（b）所示，读出数据，完成下表。答：①______________，②____________；
R/Ω | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 | 7.0 |
I/A | 0.143 | 0.125 | ① | 0.100 | 0.091 | 0.084 | 0.077 |
I-1/A-1 | 6.99 | 8.00 | ② | 10.0 | 11.0 | 11.9 | 13.0 |
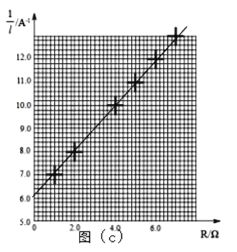
(2)将所缺数据点补充完整后并作—R图如图（c）所示，根据图线求得斜率k=__________A-1
(3)根据图线求得电源电动势E=___________V ，内阻r=___________Ω。
