题目内容
半径为R的圆与高为2R、底面半径为R的圆柱体内切，O、a为其两切点，O为底面圆心。在圆上有b点，圆柱体上有c点，a、b、c与O点间均有光滑直杆轨道，杆上穿有小球（视为质点）l、2、3。Oa、Oc与水平面夹角分别为45°和60°，同时释放小球，它们各自从a、b、c运动到O点，则
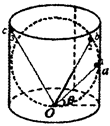
| A．2小球先到达 | B．1、2、3小球同时到达 |
| C．1、3小球最先且同时到达 | D．1、2小球最先且同时到达 |
D
设斜面与水平方向的夹角为θ，对小球受力分析，得小球沿斜面运动的加速度为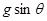
，对于同一圆周上的弦长为2Rsinθ，由运动学公式可得
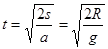，与角度无关，D正确；
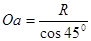，加速度为
，运动时间为
，
，加速度为
，运动时间为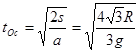
，ABC错误。
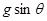，对于同一圆周上的弦长为2Rsinθ，由运动学公式可得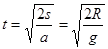，与角度无关，D正确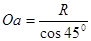；，加速度为，运动时间为，，加速度为，运动时间为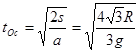，ABC错误。
练习册系列答案
智能训练练测考系列答案
计算高手系列答案
相关题目
