题目内容
如图所示,两个质量不同的小球用长度不等的细线拴在同一点并在同一水平面内做匀速圆周运动则它们的( )
| A.运动周期不同 | B.运动的线速度相同 |
| C.运动的角速度相同 | D.向心加速度相同 |
C
解析试题分析:解决本题的关键是要对球受力分析,找向心力来源,求角速度;同时要灵活应用角速度与线速度、周期、向心加速度之间的关系公式.对其中一个小球受力分析,如图,受重力,绳子的拉力,由于小球做匀速圆周运动,故合力提供向心力.
将重力与拉力合成,合力指向圆心,由几何关系得,合力:
由向心力公式得到,
设球与悬挂点间的高度差为h,由几何关系,得: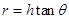
由以上三式得, ,与绳子的长度和转动半径无关,故C正确;又由
,与绳子的长度和转动半径无关,故C正确;又由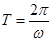 ,故A错误;由
,故A错误;由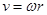 ,两球转动半径不等,故B错误;由
,两球转动半径不等,故B错误;由 ,两球转动半径不等,故D错误;所以选C.
,两球转动半径不等,故D错误;所以选C.
考点:本题考查牛顿第二定律在圆周运动中的应用以及对向心力、线速度、角速度和周期、向心加速度的理解.

练习册系列答案
相关题目
如图,当汽车通过拱桥顶点的速度为10m/s时,车对桥顶的压力为车重的3/4,如果要使汽车在桥面行驶至桥顶时,对桥面的压力为零,则汽车通过桥顶的速度应为 ( ) 
| A.15m/s | B.20m/s | C.25m/s | D.30m/s |
在匀速圆周运动中,保持不变的物理量是
| A.周期 | B.线速度 | C.加速度 | D.向心力 |



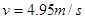




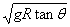

 ,它们与轴的距离关系是
,它们与轴的距离关系是 ,三物体与转盘表面的动摩擦因数相同,设最大静摩擦力等于滑动摩擦力,当转盘的转速逐渐增大时
,三物体与转盘表面的动摩擦因数相同,设最大静摩擦力等于滑动摩擦力,当转盘的转速逐渐增大时



