题目内容
在高速公路的拐弯处，路面要求筑得外高内低，即当车向右转弯时，司机左侧的路面比右侧的要高一些。设路面与水平面间的夹角为θ，拐弯路段是半径为R的圆弧，要使车轮与路面之间的横向(即垂直于前进方向)摩擦力等于零，车速大小v应等于
A． | B． |
C． | D． |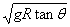
D
解析试题分析：此时重力与支持力合力恰好提供汽车做匀速圆周运动的向心力，
汽车受力分析如图所示，
则：
，
得：
考点：牛顿第二定律在圆周运动中的应用
习题精选系列答案2012年7月26日，一个国际研究小组借助于智利的甚大望远镜，观测到了一组双星系统，它们绕两者连线上的某点O做匀速圆周运动，如图所示。此双星系统中体积较小成员能“吸食”另一颗体积较大星体表面物质，达到质量转移的目的，假设在演变的过程中两者球心之间的距离保持不变，则在最初演变的过程中（两星体密度相当）
| A．它们做圆周运动的万有引力保持不变 |
| B．它们做圆周运动的角速度不断变大 |
| C．体积较大星体圆周运动轨迹半径变大，线速度也变大 |
| D．体积较大星体圆周运动轨迹半径变大，线速度变小 |
≤
如图所示的靠轮传动装置中右轮半径为2r，a为它边缘上的一点，b为轮上的一点，b距轴为r。左侧为一轮轴，大轮的半径为4r，d为它边缘上的一点，小轮的半径为r，c为它边缘上的一点。若传动中靠轮不打滑，则 
| A．a点与c点的线速度大小相等 |
| B．b点与d点的线速度大小相等 |
| C．a点与d点的向心加速度大小之比为1︰8 |
| D．c点与b点的角速度大小相等 |
如图所示，在匀速转动的水平圆盘上，沿半径方向放着用细线相连的质量相等的两个物体A和B，它们与盘间的摩擦因数相同，当圆盘转动到两个物体刚好还未发生滑动时，烧断细线，两个物体的运动情况是 （ ）
| A．两物体沿切向方向滑动 |
| B．两物体均沿半径方向滑动，离圆盘圆心越来越远 |
| C．两物体仍随圆盘一起做圆周运动，不发生滑动 |
| D．物体B仍随圆盘一起做匀速圆周运动，物体A发生滑动，离圆盘圆心越来越远 |
一偏心轮绕垂直纸面的轴O匀速转动，a和b是轮上质量相等的两个质点，a、b两点的位置如图所示，则偏心轮转动过程中a、b两质点 
| A．线速度大小相等 |
| B．向心力大小相等 |
| C．角速度大小相等 |
| D．向心加速度大小相等 |
如图所示，两个质量不同的小球用长度不等的细线拴在同一点并在同一水平面内做匀速圆周运动则它们的（ ）
| A．运动周期不同 | B．运动的线速度相同 |
| C．运动的角速度相同 | D．向心加速度相同 |
如图所示，长0.5m的轻质细杆，其一端固定于O点，另一端固定有质量为1kg的小球。小球在竖直平面内绕O点做圆周运动。已知小球通过最高点时速度大小为2m/s，运动过程中小球所受空气阻力忽略不计，g取10m/s
。关于小球通过最高点时杆对小球的作用力，下列说法中正确的是
| A．杆对小球施加向上的支持力，大小为2N |
| B．杆对小球施加向上的支持力，大小为18N |
| C．杆对小球施加向下的拉力，大小为2N |
| D．杆对小球施加向下的拉力，大小为18N |