题目内容
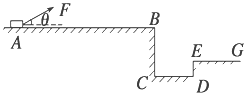
【题目】如图所示,一质量为m的物块在与水平方向成θ的力F的作用下从A点由静止开始沿水平直轨道运动,到B点后撤去力F,物体飞出后越过“壕沟”落在平台EG段.已知物块的质量m=1 kg,物块与水平直轨道间的动摩擦因数为μ=0.5,AB段长L=10 m,BE的高度差h=0.8 m,BE的水平距离x=1.6 m.若物块可看做质点,空气阻力不计,g取10 m/s2.
(1)要越过“壕沟”,求物块在B点最小速度v的大小;
(2)若θ=37°,为使物块恰好越过“壕沟”,求拉力F的大小;
【答案】(1)4 m/s (2)5.27 N
【解析】(1)设运动时间为t,则有:h=![]() gt2
gt2
所以,t=![]() =0.4s
=0.4s
水平方向匀速直线运动,故有:v=x/t=4m/s
(2)设AB段加速度为a,由匀变速直线运动规律得:v2=2aL
a=![]() =0.8m/s2
=0.8m/s2
对物块受力分析,由牛顿第二定律可得:Fcosθ-μ(mg-Fsinθ)=ma
带入数据解得:F═5.27N

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目