题目内容
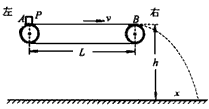
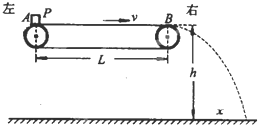 如图所示,将工件P(可视为质点)无初速地轻放在以速率v匀速运行的水平传送带的最左端A,工件P在传送带的作用下开始运动,然后从传送带最右端B飞出,落在水平地面上.已知工件P与传送带之间的动摩擦因数μ=0.1,AB的长度L=8m,B距地面的高度h=0.80m.当v=3m/s时,工件P从B端恰好水平飞出.求:
如图所示,将工件P(可视为质点)无初速地轻放在以速率v匀速运行的水平传送带的最左端A,工件P在传送带的作用下开始运动,然后从传送带最右端B飞出,落在水平地面上.已知工件P与传送带之间的动摩擦因数μ=0.1,AB的长度L=8m,B距地面的高度h=0.80m.当v=3m/s时,工件P从B端恰好水平飞出.求:(1)工件从放上传送带到落地所花的总时间(结果保留两位小数).
(2)皮带轮的半径r.
(3)若改变传送带速率v,仍能让工件水平抛出,试求出工件落地点与B点的水平距离x与速率v的函数关系式.
分析:(1)工件在传送带上只要速度小于3m/s,一直做匀加速直线运动,达到传送带速度后做匀速直线运动,离开传送带做平抛运动,根据运动学公式结合牛顿第二定律求出在传送带上运行的时间和平抛运动的时间,从而得出总时间.
(2)工件P从B端恰好水平飞出,知在B点工件所受的支持力为零,根据牛顿第二定律,通过重力提供向心力求出皮带轮的半径.
(3)求出工件一直做匀加速直线运动到达B点的速度v0,改变传送带的速率,若传送带速度v>v0,工件做匀加速直线运动,再做匀速直线运动,若v<v0,工件一直做匀加速直线运动.再根据平抛运动的规律得出水平距离x与速率v的关系.
(2)工件P从B端恰好水平飞出,知在B点工件所受的支持力为零,根据牛顿第二定律,通过重力提供向心力求出皮带轮的半径.
(3)求出工件一直做匀加速直线运动到达B点的速度v0,改变传送带的速率,若传送带速度v>v0,工件做匀加速直线运动,再做匀速直线运动,若v<v0,工件一直做匀加速直线运动.再根据平抛运动的规律得出水平距离x与速率v的关系.
解答:解:(1)工件在传送带上运动的加速度a=μg=1m/s2.
根据v2=2aL得,v=
=
m/s=4m/s>3m/s,知工件在传送带上先做匀加速直线运动,再做匀速直线运动.
匀加速直线运动的时间t1=
=
s=3s,匀加速直线运动的位移x1=
at12=
×1×9m=4.5m.
则匀速直线运动的位移x2=L-x1=8-4.5m=3.5m,则匀速运动的时间t2=
=
s=1.17s.
物体做平抛运动的时间t3=
=
s=0.4s.
则总时间t=t1+t2+t3=5.07s.
(2)根据mg=m
得,r=
=
m=0.9m.
(3)若传送带的速度v>4m/s,工件在传送带上一直做匀加速直线运动,平抛运动的初速度等于匀加速直线运动的末速度等于4m/s,
所以水平距离x=v0
=4×
m=1.6m.
若传送带的速度v<4m/s,工件在传送带上先做匀加速直线运动,再做匀速直线运动,平抛运动的初速度等于传送带的速度v,
则水平距离x=v
=0.4v.
答:(1)工件从放上传送带到落地所花的总时间为5.07s.
(2)皮带轮的半径为0.9m.
(3)若传送带的速度v>4m/s,x=1.6m,若传送带的速度v<4m/s,x=0.4v.
根据v2=2aL得,v=
| 2aL |
| 2×1×8 |
匀加速直线运动的时间t1=
| v |
| a |
| 3 |
| 1 |
| 1 |
| 2 |
| 1 |
| 2 |
则匀速直线运动的位移x2=L-x1=8-4.5m=3.5m,则匀速运动的时间t2=
| x2 |
| v |
| 3.5 |
| 3 |
物体做平抛运动的时间t3=
|
|
则总时间t=t1+t2+t3=5.07s.
(2)根据mg=m
| v2 |
| r |
| v2 |
| g |
| 9 |
| 10 |
(3)若传送带的速度v>4m/s,工件在传送带上一直做匀加速直线运动,平抛运动的初速度等于匀加速直线运动的末速度等于4m/s,
所以水平距离x=v0
|
|
若传送带的速度v<4m/s,工件在传送带上先做匀加速直线运动,再做匀速直线运动,平抛运动的初速度等于传送带的速度v,
则水平距离x=v
|
答:(1)工件从放上传送带到落地所花的总时间为5.07s.
(2)皮带轮的半径为0.9m.
(3)若传送带的速度v>4m/s,x=1.6m,若传送带的速度v<4m/s,x=0.4v.
点评:解决本题的关键理清工件在整个过程中的运动情况,结合牛顿第二定律和运动学公式进行求解.

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
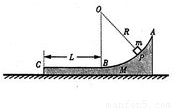
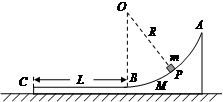 如图所示,一工件置于水平地面上,其AB段为一半径R=1.0m的光滑圆弧轨道,BC段为一长度L=0.5m的粗糙水平轨道,二者相切与B点,整个轨道位于同一竖直平面内,P点为圆弧轨道上的一个确定点.一可视为质点的物块,其质量m=0.2kg,与BC间的动摩擦因数μ1=0.4.工件质量M=0.8kg,与地面间的动摩擦因数μ2=0.1.(取g=10m/s2)
如图所示,一工件置于水平地面上,其AB段为一半径R=1.0m的光滑圆弧轨道,BC段为一长度L=0.5m的粗糙水平轨道,二者相切与B点,整个轨道位于同一竖直平面内,P点为圆弧轨道上的一个确定点.一可视为质点的物块,其质量m=0.2kg,与BC间的动摩擦因数μ1=0.4.工件质量M=0.8kg,与地面间的动摩擦因数μ2=0.1.(取g=10m/s2)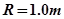 的光滑圆弧轨道,BC段为一长度
的光滑圆弧轨道,BC段为一长度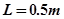 的粗糙水平轨道,二者相切与B点,整个轨道位于同一竖直平面内,P点为圆弧轨道上的一个确定点。一可视为质点的物块,其质量
的粗糙水平轨道,二者相切与B点,整个轨道位于同一竖直平面内,P点为圆弧轨道上的一个确定点。一可视为质点的物块,其质量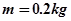 ,与BC间的动摩擦因数
,与BC间的动摩擦因数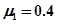 。工件质
。工件质 ,与地面间的动摩擦因数
,与地面间的动摩擦因数 。(取
。(取