Question

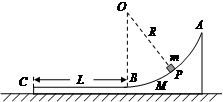如图所示，一工件置于水平地面上，其AB段为一半径R=1.0m的光滑圆弧轨道，BC段为一长度L=0.5m的粗糙水平轨道，二者相切与B点，整个轨道位于同一竖直平面内，P点为圆弧轨道上的一个确定点．一可视为质点的物块，其质量m=0.2kg，与BC间的动摩擦因数μ₁=0.4．工件质量M=0.8kg，与地面间的动摩擦因数μ₂=0.1．（取g=10m/s²）
（1）若工件固定，将物块由P点无初速度释放，滑至C点时恰好静止，求P、C两点间的高度差h．
（2）若将一水平恒力F作用于工件，使物体在P点与工件保持相对静止，一起向左做匀加速直线运动．求F的大小．

Answer 1

分析：（1）物块从P点下滑经B点至C点的整个过程，根据动能定理求解高度差h．
（2）先对物体，运用牛顿第二定律求出加速度，再对工件和物体整体分析，根据牛顿第二定律求解．题中要运用几何关系求出P点与圆心的连线与竖直方向间的夹角．

解答：解：（1）物块从P点下滑经B点至C点的整个过程，根据动能定理得 mgh-μ₁mgL=0…①
代入数据得：
h=0.2m…②
（2）①设物块的加速度大小为a，P点与圆心的连线与竖直方向间的夹角为θ，由几何关系可得
cosθ=

R-h

R

                         ③
根据牛顿第二定律，对物体有mgtanθ=ma                       ④
对工件和物体整体有 F-μ₂（M+m）g=（M+m）a        ⑤
联立②③④⑤式，代入数据得 F=8.5N
答：
（1）P、C两点间的高度差h是0.2m．
（2）F的大小是8.5N．

点评：该题考查了动能定理、牛顿第二定律多个知识点，关键要对物体进行受力和过程分析．