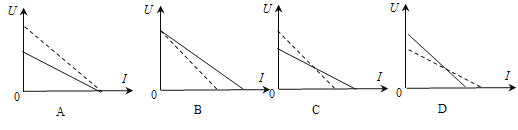
题目内容
【题目】北斗卫星导航系统是我国着眼于国家安全和经济社会发展需要,自主建设、独立运行的卫星导航系统,目前有32颗正常运行。其中地球静止轨道卫星(GEO)5颗,定点位置为东经58.75°、80°、110.5°、140°、160°的赤道上空;倾斜地球同步卫星(IGSO)7颗,均在倾角55°的轨道面上;中地球轨道卫星(MEO)20颗,运行在3个倾角为55°的轨道面上。如图所示是一颗地球静止轨道卫星A、一颗倾斜地球同步卫星B和一颗中地球轨道卫星C的轨道立体对比示意图,其中卫星B、C的轨道共面,它们都绕地球做匀速圆周运动。已知卫星C的离地高度为h,地球自转周期为T,地球半径为R,地球表面重力加速度g,万有引力常量为G,下列判断正确的是( )
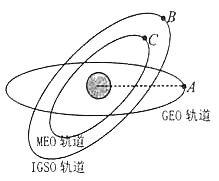
A.地球静止轨道卫星A的离地高度为![]()
B.中地球轨道卫星C的周期为![]()
C.卫星C所受的向心力大于卫星B所受的向心力
D.卫星C的线速度小于卫星B的线速度
【答案】A
【解析】
地面上的物体,重力近似等于万有引力,由牛顿第二定律:
mg=G![]()
解得:
GM=gR2
A.对地球静止轨道卫星A,万有引力提供向心力,由牛顿第二定律:
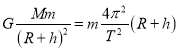
解得A离地面的高度为:
![]()
故A符合题意。
B.对卫星C,万有引力提供向心力,由牛顿第二定律:
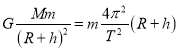
解得:

故B不符合题意。
C.对B和卫星C,由万有引力公式:F=![]() ,C卫星的半径小于B卫星的半径,但两颗卫星的质量未知,所以不能确定向心力大小,故C不符合题意。
,C卫星的半径小于B卫星的半径,但两颗卫星的质量未知,所以不能确定向心力大小,故C不符合题意。
D.由v=![]() 知,r越小,v越大,因为卫星C的运动半径小于卫星B的运动半径,所以卫星C的线速度大于卫星B的线速度,故D不符合题意。
知,r越小,v越大,因为卫星C的运动半径小于卫星B的运动半径,所以卫星C的线速度大于卫星B的线速度,故D不符合题意。

练习册系列答案
相关题目