题目内容
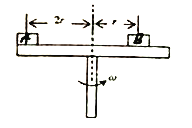
【题目】如图所示，叠放在水平转台上的物体A、B能随转台一起以角速度
匀速转动，A、B的质量分别为m、2m，A和B与转台间的动摩擦因数均为
，A与转台中心的距离为2r，B与转台中心的距离为r。设最大静摩擦力等于滑动摩擦力，则下列说法正确的是（ ）
A. 转台对A的摩擦力一定为
B. 转台对B的摩擦力一定为
C. 转台对A的摩擦力一定大于对B的摩擦力
D. 转台的角速度逐渐增大的过程中，A比B先滑动
【答案】BD
【解析】A、B两物体随转台一起做匀速转动，角速度相等，由静摩擦力提供向心力，对A物体，摩擦力不一定达到最大静摩擦力，则不一定等于μmg，对B物体，摩擦力的大小fB＝2mrω2，故A错误，B正确；对B：根据牛顿第二定律得：μmg=mrω2，解得发生滑动的临界角速度为：
，由于A的转动的半径大，可知角速度增大，A先发生相对滑动，故D正确。由于A、B未发生滑动，根据牛顿第二定律得：f=mrω2，转台对A的摩擦力大小等于对B的摩擦力大小，故C错误。所以BD正确，AC错误。
练习册系列答案
相关题目
