题目内容
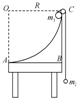
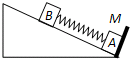
如图,一倾角为θ=30°的足够长固定光滑斜面底端有一与斜面垂直的挡板M,物块A、B之间用一与斜面平行的轻质弹簧连接且静止在斜面上.现用外力沿斜面向下缓慢推动物块B,当弹簧具有5J的弹性势能时撤去推力,释放物块B.已知物块A、B的质量分别为5kg和10kg,弹簧的弹性势能的表达式为EP=
kx2,其中弹簧的劲度系数为k=1000N/m,x为弹簧的形变量,g=10m/s2.求
(1)撤掉外力时,物块B的加速度大小;
(2)外力在推动物块B的过程中所做的功;
(3)试判断物块A能否离开挡板M?若A能离开挡板M,求出物块A刚离开挡板M时,物块B的动能;若A不能离开挡板M,求出物块A与挡板M之间的最小作用力.
| 1 |
| 2 |
(1)撤掉外力时,物块B的加速度大小;
(2)外力在推动物块B的过程中所做的功;
(3)试判断物块A能否离开挡板M?若A能离开挡板M,求出物块A刚离开挡板M时,物块B的动能;若A不能离开挡板M,求出物块A与挡板M之间的最小作用力.

(1)弹簧具有的势能为EP=5J,
EP=
kx12=
×1000x12=5,
解得,弹簧的压缩量:x1=0.1m,
撤掉外力时,由牛顿第二定律得:
kx1-mBgsinθ=mBa,
解得,物块B的加速度:a=5m/s2;
(2)物块B静止在斜面上时,
由平衡条件得:kx0=mBgsinθ,
解得:x0=0.05m,
外力推动物块B所做的功:
W=EP-
kx02-mBgsinθ(x1-x0),
代入数据解得:W=1.25J;
(3)假设物块A刚好离开挡板M,
弹簧的伸长量x2kx2=mAgsinθ,
解得:x2=0.025m,
此时弹簧的弹性势能和重力势能的增加量之和:
E=
kx22+mBgsinθ(x1+x2)=6.5625J>EP=5J,
故物块A未离开挡板M.
设物块B上滑到速度为零时,弹簧的形变量为x3
若弹簧处于压缩状态:EP=
kx32+mBgsinθ(x1-x3),
x31=0,x32=0.1m(不合理舍掉),
若弹簧处于伸长状态:EP=
kx32+mBgsinθ(x1+x3)
解得:x31=0,x32=-0.1m(不合理舍掉),
综上可得,物块B的速度为零时,弹簧恰好处于原长,
此时物块A对挡板的作用力最小,作用力F=mAgsinθ=25N;
答:(1)撤掉外力时,物块B的加速度为5m/s2;
(2)外力在推动物块B的过程中所做的功为1.25J;
(3)物块A不能离开挡板M;物块A与挡板M之间的最小作用力为25N.
EP=
| 1 |
| 2 |
| 1 |
| 2 |
解得,弹簧的压缩量:x1=0.1m,
撤掉外力时,由牛顿第二定律得:
kx1-mBgsinθ=mBa,
解得,物块B的加速度:a=5m/s2;
(2)物块B静止在斜面上时,
由平衡条件得:kx0=mBgsinθ,
解得:x0=0.05m,
外力推动物块B所做的功:
W=EP-
| 1 |
| 2 |
代入数据解得:W=1.25J;
(3)假设物块A刚好离开挡板M,
弹簧的伸长量x2kx2=mAgsinθ,
解得:x2=0.025m,
此时弹簧的弹性势能和重力势能的增加量之和:
E=
| 1 |
| 2 |
故物块A未离开挡板M.
设物块B上滑到速度为零时,弹簧的形变量为x3
若弹簧处于压缩状态:EP=
| 1 |
| 2 |
x31=0,x32=0.1m(不合理舍掉),
若弹簧处于伸长状态:EP=
| 1 |
| 2 |
解得:x31=0,x32=-0.1m(不合理舍掉),
综上可得,物块B的速度为零时,弹簧恰好处于原长,
此时物块A对挡板的作用力最小,作用力F=mAgsinθ=25N;
答:(1)撤掉外力时,物块B的加速度为5m/s2;
(2)外力在推动物块B的过程中所做的功为1.25J;
(3)物块A不能离开挡板M;物块A与挡板M之间的最小作用力为25N.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目