题目内容
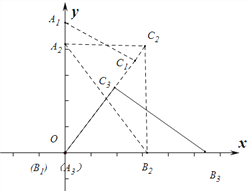
【题目】如图,直角三角板ABC的边长BC=a,AC=b,开始时,斜边AB靠在y轴上,B与坐标原点O重合,今使A点单调地沿Y轴负方向朝O点移动,B点单调地沿X轴正方向移动。A运动到原点O时,求C点通过的路程 ___________________。

【答案】 ![]()
【解析】如图,延长CA交X轴于点E,连接OC.
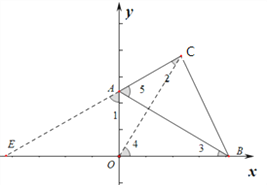
∵∠AOB=∠ACB=90°,
∴∠AOC+∠ACB=180°,∠CAO+∠CBO=180°
∵∠1+∠CAO=180°,∴∠1=∠CBO,
∵∠AEO=∠BEC,∴△AEO∽△BEC,
∴![]() ,∴
,∴![]() ,
,
∵∠AEO=∠BEC,∴△ECO∽△EBA,
∴∠2=∠3,∵∠ADC=∠ODB,∠2+∠5+∠ADC=180°,∠3+∠4+∠ODB=180°,
∴∠5=∠4,∵∠5是定值,∴∠4也是定值,
即∠COB是定值,∴点C在射线OC上运动,即C点的运动为往返的直线.
点C往返运动的路径,如图,C1到C2再到C3,
路径=C1C2+C2C3=(![]() -a)+(
-a)+(![]() -b)=2
-b)=2![]() -a-b
-a-b

练习册系列答案
相关题目