题目内容
如图所示,电阻忽略不计的、两根两平行的光滑金属导轨竖直放置,导轨间的距离为d,其上端接一电阻R,在两导轨间存在与平面垂直的匀强磁场B,且磁场区域足够大,在其下方存在与导轨相连的两个竖直的平行金属板。在两金属板间存在一光滑的轨道,倾斜轨道与水平方向的夹角为θ,倾斜轨道与竖直圆形轨道间用一段光滑小圆弧相连,圆形轨道的半径为r,将一电阻也为R、质量为m的导体棒从一位置由静止开始在导轨上无摩擦向下滑动,当导体棒开始匀速运动时,将一带正电的小球由倾斜轨道的某一位置由静止释放,小球的电荷量为q,求:

(1)导体棒匀速运动的速度;
(2)若小球到达圆形轨道最高点时对轨道的压力刚好为零,则释放小球的初位置到圆形轨道最低点的高度h多大?

(1)导体棒匀速运动的速度;
(2)若小球到达圆形轨道最高点时对轨道的压力刚好为零,则释放小球的初位置到圆形轨道最低点的高度h多大?
(1)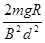 ,(2)
,(2) 。
。
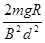 ,(2)
,(2) 。
。(原创,电学,16分)
(1)当导体棒匀速运动时,其感应电动势为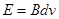 (2分)
(2分)
由闭合电路欧姆定律得: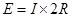 (1分)
(1分)
由平衡条件得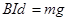 (2分)
(2分)
解得: (2分)
(2分)
(2)两板间的电势差为: (1分)
(1分)
两板间的电场强度为: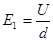 (2分)
(2分)
由动能定理得: (2分)
(2分)
在轨道最高点,由牛顿第二定律得: (2分)
(2分)
解得: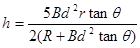 (2分)
(2分)
(1)当导体棒匀速运动时,其感应电动势为
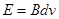 (2分)
(2分)由闭合电路欧姆定律得:
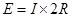 (1分)
(1分)由平衡条件得
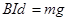 (2分)
(2分)解得:
 (2分)
(2分)(2)两板间的电势差为:
 (1分)
(1分)两板间的电场强度为:
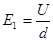 (2分)
(2分)由动能定理得:
 (2分)
(2分)在轨道最高点,由牛顿第二定律得:
 (2分)
(2分)解得:
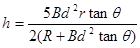 (2分)
(2分)
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目





 , 求它的横坐标的数值。
, 求它的横坐标的数值。
