题目内容
如图5所示,在水平正交的匀强电场和匀强磁场中,半径为R的光滑绝缘竖直圆环上,套有一个带正电的小球,已知小球所受电场力与重力相等,小球在环顶端A点由静止释放,当小球运动的圆弧为周长的几分之几时,所受磁场力最大?

小球下滑的过程中,要使磁场力最大,则需要速度最大。OC为与小球受到的重力、电场力的合力平行的半径。由功能关系寻找速度最大的点,因为洛伦兹力不做功,所以不考虑磁场的作用,从图中A到C,上述合力有切向分力,且与速度同向,因此做正功,小球动能增加;在C点时,该合力为径向,没有切向分力;此后切向分力与线速度反向,动能将减小;故在C点时速度最大,所受磁场力也最大。由受力分析知
mg=qE mg=qEtanα 得α= 45°
由图知θ=α+90°=135°
故小球运动的弧长与周长之比为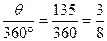 ,
,
所以运动的弧长为周长的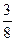 。
。
点评:讨论带电粒子的运动,必须熟悉各种力做功的特点。该题也可用等效法处理。把电场和重力场合起来当作一个新的重力场,这个重力场的竖直方向与原水平方向成45°角斜向下,这样就很容易确定速度最大的点。
mg=qE mg=qEtanα 得α= 45°
由图知θ=α+90°=135°
故小球运动的弧长与周长之比为
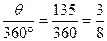 ,
,所以运动的弧长为周长的
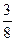 。
。点评:讨论带电粒子的运动,必须熟悉各种力做功的特点。该题也可用等效法处理。把电场和重力场合起来当作一个新的重力场,这个重力场的竖直方向与原水平方向成45°角斜向下,这样就很容易确定速度最大的点。

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目






