��Ŀ����
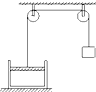
����Ŀ����ͼ��ʾ��б����ABC�̶��ڵ����ϣ�С��p��A�㾲ֹ�»�����С��p��ʼ�»���ͬʱ����һС��q��A�����Ϸ���D��ˮƽ�׳�������ͬʱ����б��˵�B������֪б��AB�⻬������l=0.75m��б�������=37�������ƿ�����������
��gȡ10m/s2��sin37��=0.6��cos37��=0.8��
��1��С��p��A�㻬��B������Ҫ��ʱ�䣻
��2��С��q�׳�ʱ���ٶȵĴ�С��

���𰸡���1��0.5s����2��1.2m/s��
����������1��С��p��б�����»��ļ��ٶ�Ϊa����ţ�ٵڶ������У� ![]()
���»�����ʱ��Ϊt1�������˶�ѧ��ʽ�У� ![]()
������ã�t1 =0.5 s .
��2��С��q��ƽ���˶������׳��ٶ�Ϊv0����
![]()
�ɼ��ι�ϵ֪��x=lcos37��
�������� t2=t1
��ã� v0=1.2m/s
�㾦: �������ȼ���ֱ���˶���ƽ���˶����ۺϣ���Ҫ�ֱ��о�����������˶��������Ҫץס�����˶���ͬʱ�ԣ�

��ϰ��ϵ�д�
 ��ʦ����ɳ���ʱͬ��ѧ����ϵ�д�
��ʦ����ɳ���ʱͬ��ѧ����ϵ�д�
�����Ŀ