题目内容
有两个光滑固定的斜面AB和BC,A和C两点在同一水平面上,斜面BC比斜面AB长(如图),一个滑块自A点以速度vA上滑,到达B点时速度减小为零,紧接着沿BC滑下,设滑块从A点到C点的总时间是tC,图中能正确表示滑块速度的大小v随时间t变化规律的是( )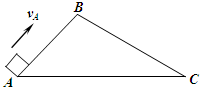
A.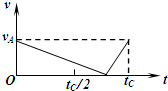 | B.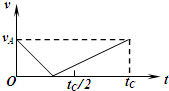 |
C.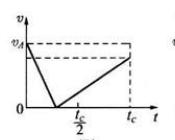 | D.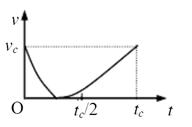 |
B
解析试题分析:设AB的加速度为a,AB与水平面的夹角为θ,则a=gsinθ,设初速度为v,则滑块由A到B可以看成由B到A的初速度为0的匀加速直线运动,则v2=2a×AB=2gsinθ×AB=2gh,h为B点的高,当滑块沿BC下滑时的滑到C点的速度v′2=2gh,故v=v′;
由于AB斜面比BC陡,所以滑块在AB上的加速度大于在BC上的加速度,又因为它们的末速度是相等的,故滑块在AB上所用的时间小于在BC上所用的时间,B是正确的。
该题也可以用能量守恒来解决,由于不计摩擦,故整个过程遵循机械能守恒定律,故A点与C点的机械能相等,由于二者处于同一高度,故它们的速度是相等的。
考点:牛顿第二定律,匀变速直线运动的规律应用。

 一线名师权威作业本系列答案
一线名师权威作业本系列答案一物体由静止沿一足够长光滑斜面匀加速下滑距离为L时,速度为v,此后继续下滑,当它的速度增至2v时,它又沿斜面继续下滑的距离是
| A.L | B.2L | C.3L | D.4L |
物体第1s由静止向东做加速度为1m/s2的匀加速直线运动,第2s加速度方向向西,大小不变,以后每隔1s加速度的方向都改变一次,但大小不变,如此反复只改变加速度的方向,共历时1 min。则在此1min内( )
| A.物体时而向东运动,时而向西运动,在1 min 末静止于初始位置之西 |
| B.物体一直向东运动,从不向西运动,在1 min 末静止于初始位置之东30m的位置 |
| C.物体时而向东运动,时而向西运动,在1 min 末继续向东运动 |
| D.物体一直向东运动,从不向西运动,在1 min 末静止于初始位置之东15m的位置 |
做匀变速直线运动的质点,它的位移随时间变化的规律是x=(24t-1.5t2)m,则质点的速度为零的时刻是( )
| A.1.5s | B.8s | C.16s | D.24s |
某一时刻a、b两物体以不同的速度经过某一点,并沿同一方向做匀加速直线运动,已知两物体的加速度相同,则在运动过程中( )
| A.a、b两物体速度之差保持不变 |
| B.a、b两物体速度之差与时间成正比 |
| C.a、b两物体位移之差与时间成正比 |
| D.a、b两物体位移之差与时间平方成正比 |
一物体沿光滑斜面由静止开始匀加速下滑,当下滑距离为L时,物体速度为v,当物体的速度是v/2时,它沿斜面下滑的距离是( )
| A.L/4 | B.L/2 | C.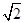 L/2 L/2 | D.3L/4 |
如图所示,一小滑块沿足够长的斜面以初速度v向上做匀减速直线运动,依次经A,B,C,D 到达最高点E,已知AB=BD=6m,BC=1m,滑块从A到C和从C到D所用的时间都是2s .设滑块经C时的速度为vc,则( )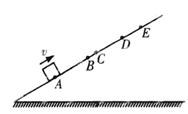
| A.滑块上滑过程中加速度的大小为0.5m/s2 |
| B.vc =6m/s |
| C.DE=3m |
| D.从D到E所用时间为4s |
如图所示,ad、bd、 cd是竖直面内的三根固定的光滑细杆,a、b、c、d位于同一圆周上,a点为圆周上最高点,d点为圆周上最低点。每根杆上都套有一个小圆环,三个圆环分别从a、b、c处由静止释放,用t1、t2、t3依次表示各环到达d点所用的时间,则( )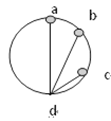
| A.t 1<t2<t3 | B.t 1>t2>t3 |
| C.t 3>t1>t2 | D.t 1=t2=t3 |