题目内容
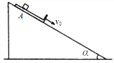
【题目】如图所示，将质量m=1.0kg的小物块放在长L=3.0m的平板车左端，车的上表面粗糙，物块与车上表面间的动摩擦因数μ=0.6,光滑半圆形固定轨道与光滑水平轨道在同一竖直平面内，半圆形轨道的半径r=l. 2m,直径MON竖直，车的上表面和轨道最低点高度相同，开始时车和物块一起以v0=10m/s的初速度在水平轨道上向右运动，车碰到轨道后立即停止运动，取 g=10m/s2，求：
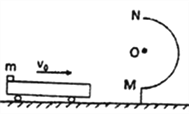
(1)物块刚进入半圆形时速度大小：
(2)物块刚进入半圆形时对轨道的压力大小；
(3)物块回落至车上时距右端的距离。
【答案】（1）8.0m/s （2）2.8m
【解析】试题分析：选取物块为研究对象应用动能定理即可求得速度；物块做圆周运动，由牛顿第二定律和向心力公式列式可以求出物块受到的支持力，然后由牛顿第三定律求出对轨道的压力；小物块从车上滑下做平抛运动，根据平抛运动的基本公式即可求解。
（1）车停止运动后取小物块为研究对象，设其到达车右端时的速度为v1，由动能定理可得：
，解得v1=8.0m/s
（2）刚进入半圆轨道时，设物块受到的支持力为FN,由牛顿第二定律：
，代入数据解得：
. 由牛顿第三定律可得：
，所以物块刚进入半圆轨道时对轨道的压力为63.3N,方向竖直向下.
（3）若物块能到达半圆形轨道的最高点，则由机械能守恒可得：
解得v2=4m/s
设恰能通过最高点的速度为v3，则：
代入数据解得：
因v2>v3，故小物块从半圆轨道最高点做平抛运动，设距车右端的水平距离为x,则：
在竖直方向：
水平方向：
代入数据解得：
练习册系列答案
名校课堂系列答案
相关题目
