��Ŀ����
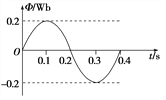
����Ŀ����ͼ��ʾ���⻬б������a=30�㣬��б���Ϸ���һ�����߿�abcd��ab�ߵı߳�l1=1m��bc�ߵı߳�l2=0.6m���߿������m=1kg������R=0.1�����߿��ܵ��ع⻬б�����ϵĺ���F�����ã���֪F=10N��б����ef�ߣ�ef��gh�����ҷ��д�ֱб�����ϵľ��ȴų����Ÿ�Ӧǿ��B��ʱ��t�ı仯�����B��tͼ����ʾ��ʱ��t�Ǵ��߿��ɾ�ֹ��ʼ�˶�ʱ����Ƶģ�����߿�Ӿ�ֹ��ʼ�˶�������ų����һ��ʱ�������ٵģ�ef�ߺ�gh�ľ���s=5.1m��ȡ g=10m/s2����
��1���߿����ų�ǰ�ļ��ٶȣ�
��2���߿����ų�ʱ�����˶����ٶ�v��
��3���߿��������ų���ab���˶���gh�ߵĹ����в����Ľ����ȣ�

���𰸡���1���߿���˴ų�ǰ�ļ��ٶ���5m/s2��
��2 ���߿���˴ų�ʱ�����˶����ٶ�v��2m/s��
��3���߿��������ų���ab���˶���gh�ߵĹ����в����Ľ�������0.5J��
�������������������1���߿����ų�ǰ���ܵ�������ϸ�ߵ�����F��б���֧�����������ȼ����˶�������ţ�ٵڶ����������ٶȣ�
��2���߿���˴ų����һ��ʱ�������ٵģ�����Ϊ�㣬��E=Blv��I=![]() ��F=BIl�Ƶ�������������ʽ����ƽ����������ٶȣ�
��F=BIl�Ƶ�������������ʽ����ƽ����������ٶȣ�
��3���߿����ų�ǰ���ȼ���ֱ���˶������ų��Ĺ�����������ֱ���˶����ֱ��ɹ�ʽ����߿����ų�ǰ�˶���ʱ��ͽ��ų������˶���ʱ�䣮�߿���ȫ����ų���������������ų�ǰ��ͬ�����ٶ���ͬ������λ�ƹ�ʽ����gh�˶���ef��ʱ�䣬���ͼ������߿��������ų���ab���˶���gh�ߵĹ������и�Ӧ������ʱ�䣬���ݷ����ڶ�����ø�Ӧ�綯�ƣ��ɽ����������������
�⣺��1���߿����ų�ǰ���ܵ�������ϸ�ߵ�����F��б���֧�����������ȼ����˶�������ţ�ٵڶ����ɵ�
F��mgsin��=ma
�ã�a=![]() =5m/s2
=5m/s2
��2���߿���˴ų����һ��ʱ�������ٵģ�����Ϊ�㣬��E=Bl1v��I=![]() ��FA=BIl1 �ð�����Ϊ
��FA=BIl1 �ð�����Ϊ
FA=![]()
����ƽ�������� F=mgsin��+FA=mgsin��+![]()
������ v=2m/s
��3���߿�abcd����ų�ǰ���ȼ����˶������ų��Ĺ����У��������˶�������ų����˶���gh�������ȼ����˶���
���ų�ǰ�߿���˶���ʱ��Ϊt1=![]() =
=![]()
���ų������������˶���ʱ��Ϊt2=![]() =
=![]() s=0.3s
s=0.3s
�߿���ȫ����ų����߿�������������ų�ǰ��ͬ�����Ըýεļ��ٶ���Ϊa=5m/s2��
��s��l2=vt3+![]()
��ã�t3=1s
����߿��������ų���ab���˶���gh�ߵĹ������и�Ӧ������ʱ��Ϊt4=1����0.9��t1��t2��=0.8s
�߿��в����ĸ�Ӧ�綯��Ϊ E=![]() =
=![]() =
=![]() V=0.25V
V=0.25V
�߿��������ų���ab���˶���gh�ߵĹ����в����Ľ�����Ϊ
Q=![]() =
=![]() J=0.5J
J=0.5J
��
��1���߿���˴ų�ǰ�ļ��ٶ���5m/s2��
��2 ���߿���˴ų�ʱ�����˶����ٶ�v��2m/s��
��3���߿��������ų���ab���˶���gh�ߵĹ����в����Ľ�������0.5J��