题目内容
15.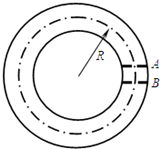 如图所示为一种获得高能粒子的装置.A、B为两块中心开有小孔的极板,每当带电粒子经过A、B板时,都会被加速.其原理如下:当粒子飞到A板小孔时,A、B板间的加速电压变为U;每当粒子飞离电场后即做匀速圆周运动,A、B板间的电势差立即变为零.粒子在A、B间的电场中一次次被加速,动能不断增大,并保持匀速圆周运动半径R不变(A、B两极板间的距离远小于R).当t=0时,质量为m、电荷量为+q的粒子正好静止在A板小孔处,不考虑带电粒子重力的影响.若两板间距为d,则该粒子第一次飞过两板间所需时间为d$\sqrt{\frac{2m}{qU}}$;该粒子第九次和第十次飞过两板间所需时间之比为(3-$\sqrt{8}$):($\sqrt{10}$-3)(无需分母有理化).
如图所示为一种获得高能粒子的装置.A、B为两块中心开有小孔的极板,每当带电粒子经过A、B板时,都会被加速.其原理如下:当粒子飞到A板小孔时,A、B板间的加速电压变为U;每当粒子飞离电场后即做匀速圆周运动,A、B板间的电势差立即变为零.粒子在A、B间的电场中一次次被加速,动能不断增大,并保持匀速圆周运动半径R不变(A、B两极板间的距离远小于R).当t=0时,质量为m、电荷量为+q的粒子正好静止在A板小孔处,不考虑带电粒子重力的影响.若两板间距为d,则该粒子第一次飞过两板间所需时间为d$\sqrt{\frac{2m}{qU}}$;该粒子第九次和第十次飞过两板间所需时间之比为(3-$\sqrt{8}$):($\sqrt{10}$-3)(无需分母有理化).
分析 根据粒子在MN板间加速过程和在磁场中圆周运动过程,结合动能定理,即可求得加速n次的总时间,从而即可求解.
解答 解:粒子在每一圈的运动过程中,包括在MN板间加速过程和在磁场中圆周运动过程.
在MN板间经历n次加速过程中,因为电场力大小相同,故有:nd=$\frac{1}{2}$•$\frac{qU}{md}$•${t}_{加}^{2}$
即加速n次的总时间 t加=d$\sqrt{\frac{2nm}{qU}}$
因此第一飞过两板间所需时间为t1=d$\sqrt{\frac{2m}{qU}}$;
当粒子第九次和第十次飞过两板间所需时间之比为t9:t10=($\sqrt{9}$-$\sqrt{8}$):($\sqrt{10}$-$\sqrt{9}$)=(3-$\sqrt{8}$):($\sqrt{10}$-3);
故答案为:d$\sqrt{\frac{2m}{qU}}$;(3-$\sqrt{8}$):($\sqrt{10}$-3).
点评 考查粒子在电场中加速,与磁场中偏转,电场力做功,而磁场力不做功,掌握动能定理的应用,注意求得加速n次的总时间是解题的关键.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
相关题目
5. 如图所示,弹性橡皮绳下悬挂一个小球,处于静止状态.现将一个倾斜的光滑木板与球轻轻接触,把木板缓慢竖直向上移动,移动过程中木板倾角不变,在橡皮绳平行木板前,下列说法正确的是( )
如图所示,弹性橡皮绳下悬挂一个小球,处于静止状态.现将一个倾斜的光滑木板与球轻轻接触,把木板缓慢竖直向上移动,移动过程中木板倾角不变,在橡皮绳平行木板前,下列说法正确的是( )
 如图所示,弹性橡皮绳下悬挂一个小球,处于静止状态.现将一个倾斜的光滑木板与球轻轻接触,把木板缓慢竖直向上移动,移动过程中木板倾角不变,在橡皮绳平行木板前,下列说法正确的是( )
如图所示,弹性橡皮绳下悬挂一个小球,处于静止状态.现将一个倾斜的光滑木板与球轻轻接触,把木板缓慢竖直向上移动,移动过程中木板倾角不变,在橡皮绳平行木板前,下列说法正确的是( )| A. | 球对木板的压力先增大后减小 | |
| B. | 橡皮绳的长度逐渐减小 | |
| C. | 木板对小球做的功等于小球机械能的增加量 | |
| D. | 橡皮绳对小球不做功 |
3.下列单位中属于国际单位制(SI)基本单位的是( )
| A. | 千克 | B. | 千米 | C. | 千焦 | D. | 千帕 |
10.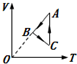 如图所示,一定质量的理想气体,经过图线A→B→C→A的状态变化过程,AB的延长线过O点,CA与纵轴平行.由图线可知( )
如图所示,一定质量的理想气体,经过图线A→B→C→A的状态变化过程,AB的延长线过O点,CA与纵轴平行.由图线可知( )
 如图所示,一定质量的理想气体,经过图线A→B→C→A的状态变化过程,AB的延长线过O点,CA与纵轴平行.由图线可知( )
如图所示,一定质量的理想气体,经过图线A→B→C→A的状态变化过程,AB的延长线过O点,CA与纵轴平行.由图线可知( )| A. | A→B过程气体压强不变,密度减小 | B. | B→C过程气体压强增大,密度增大 | ||
| C. | B→C过程气体温度升高,密度减小 | D. | C→A过程气体温度不变,密度增大 |
7.如图所示,A、B是完全相同的两个小灯泡,L为自感系数很大、电阻可以忽略的带铁芯的线圈,则( )
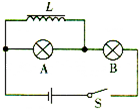

| A. | 开关S闭合瞬间,B灯亮,A灯不亮 | |
| B. | 开关S闭合瞬间,A、B同时发光,随后A灯变暗直至熄灭,B灯变亮 | |
| C. | 断开开关S的瞬间,A、B灯同时熄灭 | |
| D. | 断开开关S的瞬间,B灯立即熄灭,A灯突然闪亮一下再熄灭 |
5.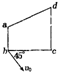 如图所示,a、b、c、d为某匀强电场中的四个点,且ab∥cd,ab⊥bc,bc=cd=2ab=2l,电场线与四边形所在平面平行.已知φa=20V,φb=24V,φd=8V.一个质子经过b点的速度大小为v0,方向与bc夹角为45°,一段时间后经过c点,e为质子的电量,不计质子的重力,则( )
如图所示,a、b、c、d为某匀强电场中的四个点,且ab∥cd,ab⊥bc,bc=cd=2ab=2l,电场线与四边形所在平面平行.已知φa=20V,φb=24V,φd=8V.一个质子经过b点的速度大小为v0,方向与bc夹角为45°,一段时间后经过c点,e为质子的电量,不计质子的重力,则( )
 如图所示,a、b、c、d为某匀强电场中的四个点,且ab∥cd,ab⊥bc,bc=cd=2ab=2l,电场线与四边形所在平面平行.已知φa=20V,φb=24V,φd=8V.一个质子经过b点的速度大小为v0,方向与bc夹角为45°,一段时间后经过c点,e为质子的电量,不计质子的重力,则( )
如图所示,a、b、c、d为某匀强电场中的四个点,且ab∥cd,ab⊥bc,bc=cd=2ab=2l,电场线与四边形所在平面平行.已知φa=20V,φb=24V,φd=8V.一个质子经过b点的速度大小为v0,方向与bc夹角为45°,一段时间后经过c点,e为质子的电量,不计质子的重力,则( )| A. | c点电势为12V | |
| B. | 场强的方向由a指向c | |
| C. | 质子从b运动到c所用的时间为 $\frac{\sqrt{2}l}{{v}_{0}}$ | |
| D. | 质子从b运动到c电场力做功12eV |

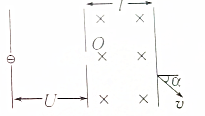 如图所示,初速度可忽略不计的电子经加速电场加速后从小孔O进入磁感应强度为B的有界磁场,磁场宽度为l,射出磁场时电子的偏转角为α,已知加速电场电势差为U,求电子的比荷.
如图所示,初速度可忽略不计的电子经加速电场加速后从小孔O进入磁感应强度为B的有界磁场,磁场宽度为l,射出磁场时电子的偏转角为α,已知加速电场电势差为U,求电子的比荷.