题目内容
4.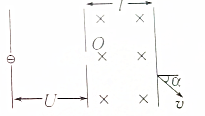 如图所示,初速度可忽略不计的电子经加速电场加速后从小孔O进入磁感应强度为B的有界磁场,磁场宽度为l,射出磁场时电子的偏转角为α,已知加速电场电势差为U,求电子的比荷.
如图所示,初速度可忽略不计的电子经加速电场加速后从小孔O进入磁感应强度为B的有界磁场,磁场宽度为l,射出磁场时电子的偏转角为α,已知加速电场电势差为U,求电子的比荷.
分析 作出粒子的运动轨迹,结合几何关系求出轨道半径的大小,从而根据洛伦兹力提供向心力求出粒子进入磁场的速度大小,通过动能定理求出加速电压的大小.
解答 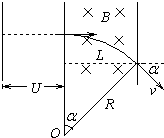 解:电子经加速电场加速后,速度为v,则由动能定理得$eU=\frac{1}{2}m{v^2}$
解:电子经加速电场加速后,速度为v,则由动能定理得$eU=\frac{1}{2}m{v^2}$
电子进入匀强磁场中作匀速圆周运动,轨迹如图,
由几何关系得,电子运动半径$R=\frac{L}{sinα}$
由牛顿第二定律,有$evB=m\frac{v^2}{R}$
由以上各式解得$\frac{e}{m}=\frac{2Usi{n}^{2}α}{{B}^{2}{L}^{2}}$
答:电子的比荷为$\frac{2Usi{n}^{2}α}{{B}^{2}{L}^{2}}$.
点评 解决本题的关键作出粒子的运动轨迹图,结合几何关系、牛顿第二定律和动能定理进行求解.

练习册系列答案
相关题目
14.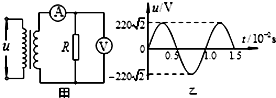 图甲中一理想变压器原、副线圈匝数之比为55:6,其原线圈两端接入如图乙所示的正弦交流电,副线圈通过电流表与阻值R=48Ω的负载电阻相连.若交流电压表和交流电流表都是理想电表,则下列说法中正确的是( )
图甲中一理想变压器原、副线圈匝数之比为55:6,其原线圈两端接入如图乙所示的正弦交流电,副线圈通过电流表与阻值R=48Ω的负载电阻相连.若交流电压表和交流电流表都是理想电表,则下列说法中正确的是( )
 图甲中一理想变压器原、副线圈匝数之比为55:6,其原线圈两端接入如图乙所示的正弦交流电,副线圈通过电流表与阻值R=48Ω的负载电阻相连.若交流电压表和交流电流表都是理想电表,则下列说法中正确的是( )
图甲中一理想变压器原、副线圈匝数之比为55:6,其原线圈两端接入如图乙所示的正弦交流电,副线圈通过电流表与阻值R=48Ω的负载电阻相连.若交流电压表和交流电流表都是理想电表,则下列说法中正确的是( )| A. | 电压表的示数是24$\sqrt{2}$V | |
| B. | 电流表的示数为0.50A | |
| C. | 变压器原线圈得到的功率是24W | |
| D. | 原线圈输入的正弦交变电流的频率是50Hz |
12.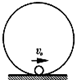 如图所示,半径r=0.5m的光滑圆轨道被竖直固定在水平地面上,圆轨道最低处有一小球(小球的半径比r小很多).现给小球一个水平向右的初速度v0,要使小球不脱离轨道运动,重力加速度g取10m/s2,则下列初速度v0范围能满足的是( )
如图所示,半径r=0.5m的光滑圆轨道被竖直固定在水平地面上,圆轨道最低处有一小球(小球的半径比r小很多).现给小球一个水平向右的初速度v0,要使小球不脱离轨道运动,重力加速度g取10m/s2,则下列初速度v0范围能满足的是( )
 如图所示,半径r=0.5m的光滑圆轨道被竖直固定在水平地面上,圆轨道最低处有一小球(小球的半径比r小很多).现给小球一个水平向右的初速度v0,要使小球不脱离轨道运动,重力加速度g取10m/s2,则下列初速度v0范围能满足的是( )
如图所示,半径r=0.5m的光滑圆轨道被竖直固定在水平地面上,圆轨道最低处有一小球(小球的半径比r小很多).现给小球一个水平向右的初速度v0,要使小球不脱离轨道运动,重力加速度g取10m/s2,则下列初速度v0范围能满足的是( )| A. | v0≥5m/s | B. | v0≥2$\sqrt{5}$m/s | C. | v0≥$\sqrt{5}$m/s | D. | v0≤$\sqrt{10}$m/s |
19.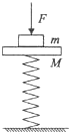 如图所示,竖直轻质弹簧,下端固定在地面,上端固定一质量为M的木板,木板上方放一质量为m的物块,木板和物块间不粘连,一竖直向下的力F作用在物块上,整个系统处于静止状态.现在撤去F,木板和物块向上运动的过程中,下列说法正确的是( )
如图所示,竖直轻质弹簧,下端固定在地面,上端固定一质量为M的木板,木板上方放一质量为m的物块,木板和物块间不粘连,一竖直向下的力F作用在物块上,整个系统处于静止状态.现在撤去F,木板和物块向上运动的过程中,下列说法正确的是( )
 如图所示,竖直轻质弹簧,下端固定在地面,上端固定一质量为M的木板,木板上方放一质量为m的物块,木板和物块间不粘连,一竖直向下的力F作用在物块上,整个系统处于静止状态.现在撤去F,木板和物块向上运动的过程中,下列说法正确的是( )
如图所示,竖直轻质弹簧,下端固定在地面,上端固定一质量为M的木板,木板上方放一质量为m的物块,木板和物块间不粘连,一竖直向下的力F作用在物块上,整个系统处于静止状态.现在撤去F,木板和物块向上运动的过程中,下列说法正确的是( )| A. | 物块先处于超重状态,再处于失重状态 | |
| B. | 木板对物块做正功,物块的机械能增加 | |
| C. | 木板和物块组成的系统机械能守恒 | |
| D. | 当木块和物块分离时,弹簧处于自然状态 |
9.M、N两颗质量相同的卫星绕地球做匀速圆周运动,其轨道如图所示,则( )
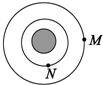

| A. | M与地球中心连线在相等的时间内转过的角度较大 | |
| B. | M的机械能大于N的机械能 | |
| C. | M、N的速度均大于第一宇宙速度 | |
| D. | M在相同的时间内经过的路程较短 |
13.以下说法中正确的是( )
| A. | 单晶体的所有物理性质都具有各向异性 | |
| B. | 悬浮在液体中的花粉颗粒的无规则运动是热运动 | |
| C. | 相同温度下,氢分子的平均动能一定等于于氧分子的平均动能 | |
| D. | 随着分子间距离增大,分子间作用力减小,分子势能也减小 |
14.A、B两艘快艇在湖面上做匀速圆周运动,在相同时间内,它们的路程之比为4:3,运动方向改变的角度之比为3:2,它们的向心加速度之比为( )
| A. | 1:2 | B. | 2:1 | C. | 4:2 | D. | 3:4 |
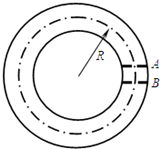 如图所示为一种获得高能粒子的装置.A、B为两块中心开有小孔的极板,每当带电粒子经过A、B板时,都会被加速.其原理如下:当粒子飞到A板小孔时,A、B板间的加速电压变为U;每当粒子飞离电场后即做匀速圆周运动,A、B板间的电势差立即变为零.粒子在A、B间的电场中一次次被加速,动能不断增大,并保持匀速圆周运动半径R不变(A、B两极板间的距离远小于R).当t=0时,质量为m、电荷量为+q的粒子正好静止在A板小孔处,不考虑带电粒子重力的影响.若两板间距为d,则该粒子第一次飞过两板间所需时间为d$\sqrt{\frac{2m}{qU}}$;该粒子第九次和第十次飞过两板间所需时间之比为(3-$\sqrt{8}$):($\sqrt{10}$-3)(无需分母有理化).
如图所示为一种获得高能粒子的装置.A、B为两块中心开有小孔的极板,每当带电粒子经过A、B板时,都会被加速.其原理如下:当粒子飞到A板小孔时,A、B板间的加速电压变为U;每当粒子飞离电场后即做匀速圆周运动,A、B板间的电势差立即变为零.粒子在A、B间的电场中一次次被加速,动能不断增大,并保持匀速圆周运动半径R不变(A、B两极板间的距离远小于R).当t=0时,质量为m、电荷量为+q的粒子正好静止在A板小孔处,不考虑带电粒子重力的影响.若两板间距为d,则该粒子第一次飞过两板间所需时间为d$\sqrt{\frac{2m}{qU}}$;该粒子第九次和第十次飞过两板间所需时间之比为(3-$\sqrt{8}$):($\sqrt{10}$-3)(无需分母有理化).