题目内容
如图甲所示,粗糙水平面CD与光滑斜面DE平滑连接于D处;可视为质点的物块A、B紧靠一起静置于P点,某时刻A、B在足够大的内力作用下突然分离,此后A向左运动.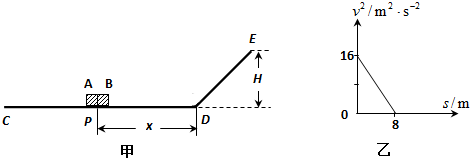
已知:斜面的高度H=1.2m;A、B质量分别为1kg和0.8kg,且它们与CD段的动摩擦因数相同;A向左运动的速度平方与位移大小关系如图乙;重力加速度g取10m/s2.
(1)求A、B与CD段的动摩擦因数μ;
(2)求A、B分离时B的速度大小vB;
(3)要使B能追上A,试讨论P、D两点间距x的取值范围.

已知:斜面的高度H=1.2m;A、B质量分别为1kg和0.8kg,且它们与CD段的动摩擦因数相同;A向左运动的速度平方与位移大小关系如图乙;重力加速度g取10m/s2.
(1)求A、B与CD段的动摩擦因数μ;
(2)求A、B分离时B的速度大小vB;
(3)要使B能追上A,试讨论P、D两点间距x的取值范围.
分析:(1)由图乙读出分离时物块A的初速度vA,及A最终位置与P点距离sA,根据牛顿牛顿第二定律和运动学公式结合,或动能定理求解动摩擦因数μ;
(2)A、B分离过程,遵守动量守恒定律,据此列式求解A、B分离时B的速度大小vB;
(3)要使B能追上A,B不能冲出斜面,恰好返回时,根据动能定理和位移关系求解x的取值范围.
(2)A、B分离过程,遵守动量守恒定律,据此列式求解A、B分离时B的速度大小vB;
(3)要使B能追上A,B不能冲出斜面,恰好返回时,根据动能定理和位移关系求解x的取值范围.
解答:解:(1)由图象可知,分离时物块A的初速度vA=4m/s,①
A最终位置与P点距离 sA=8m,②
从A、B分离到A匀减速运动停止,有vA2=2asA ③
得A的加速度大小为 a=1m/s2 ④
由牛顿第二定律可知fA=μmAg=mAa ⑤
解得:μ=0.1 ⑥
【或:从A、B分离到A匀减速运动停止,由动能定理得:-μmAgsA=0-
mA
解得:μ=0.1】
(2)A、B分离过程,取B的速度方向为正方向,由动量守恒得:
0=mBvB-mAvA ⑦
解得:vB=5m/s ⑧
(3)(Ⅰ)若B恰好能返回并追上A,B从分离后到追上A过程由动能定理得:
-μmBg(2x1+SA)=0-
mB
⑨
解得:x1=2.25m ⑩
(Ⅱ)若B恰好不冲出斜面,B从P到E过程由动能定理得:
μmBgx2-mBgH=0-
mB
解得:x2=0.50m
综上,要使B能追上A,x应满足:2.25m≥L≥0.50m
答:
(1)A、B与CD段的动摩擦因数μ为0.1;
(2)A、B分离时B的速度大小vB是5m/s.
(3)要使B能追上A,P、D两点间距x的取值范围是2.25m≥L≥0.50m.
A最终位置与P点距离 sA=8m,②
从A、B分离到A匀减速运动停止,有vA2=2asA ③
得A的加速度大小为 a=1m/s2 ④
由牛顿第二定律可知fA=μmAg=mAa ⑤
解得:μ=0.1 ⑥
【或:从A、B分离到A匀减速运动停止,由动能定理得:-μmAgsA=0-
| 1 |
| 2 |
| v | 2 A |
解得:μ=0.1】
(2)A、B分离过程,取B的速度方向为正方向,由动量守恒得:
0=mBvB-mAvA ⑦
解得:vB=5m/s ⑧
(3)(Ⅰ)若B恰好能返回并追上A,B从分离后到追上A过程由动能定理得:
-μmBg(2x1+SA)=0-
| 1 |
| 2 |
| v | 2 B |
解得:x1=2.25m ⑩
(Ⅱ)若B恰好不冲出斜面,B从P到E过程由动能定理得:
μmBgx2-mBgH=0-
| 1 |
| 2 |
| v | 2 B |
解得:x2=0.50m
综上,要使B能追上A,x应满足:2.25m≥L≥0.50m
答:
(1)A、B与CD段的动摩擦因数μ为0.1;
(2)A、B分离时B的速度大小vB是5m/s.
(3)要使B能追上A,P、D两点间距x的取值范围是2.25m≥L≥0.50m.
点评:对于复杂的力学问题,关键要能正确分析物体的运动情况,找出每个过程的规律,本题的切入口是对图象的理解,抓住图象的有效信息进行求解.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
 如图甲所示,粗糙的足够长的竖直木杆上套有一个带电的小球,整个装置处在由水平匀强电场和垂直纸面向外的匀强磁场组成的足够大的复合场中,小球由静止开始下滑,在整个运动过程中小球的v~t图象如图乙所示,其中错误的是( )
如图甲所示,粗糙的足够长的竖直木杆上套有一个带电的小球,整个装置处在由水平匀强电场和垂直纸面向外的匀强磁场组成的足够大的复合场中,小球由静止开始下滑,在整个运动过程中小球的v~t图象如图乙所示,其中错误的是( ) 如图甲所示,光滑水平面上停放着一辆上表面粗糙的平板车,平板车质量为M.一质量为m的铁块,以水平初速度v0滑到小车上,两物体开始运动,它们的速度随时间变化的图象如图乙所示(t0是滑块在车上运动的时间),则可以断定( )
如图甲所示,光滑水平面上停放着一辆上表面粗糙的平板车,平板车质量为M.一质量为m的铁块,以水平初速度v0滑到小车上,两物体开始运动,它们的速度随时间变化的图象如图乙所示(t0是滑块在车上运动的时间),则可以断定( )
 如图甲所示,粗糙物块A、B叠放在粗糙的水平桌面上,水平外力F作用在A上,甲乙使A、B一起沿水平桌面向右加速运动.设A、B之间的摩擦力为f1,B与水平桌面间的摩擦力为f2.在始终保持A、B相对静止的情况下,逐渐增大F;又如图乙所示,同样的物块A、B叠放在粗糙的水平桌面上,水平外力F作用在A上,使A向右加速运动而B不动.设A、B之间的摩擦力为f3,B与水平桌面间的摩擦力为f4,逐渐增大F.则( )
如图甲所示,粗糙物块A、B叠放在粗糙的水平桌面上,水平外力F作用在A上,甲乙使A、B一起沿水平桌面向右加速运动.设A、B之间的摩擦力为f1,B与水平桌面间的摩擦力为f2.在始终保持A、B相对静止的情况下,逐渐增大F;又如图乙所示,同样的物块A、B叠放在粗糙的水平桌面上,水平外力F作用在A上,使A向右加速运动而B不动.设A、B之间的摩擦力为f3,B与水平桌面间的摩擦力为f4,逐渐增大F.则( )