题目内容
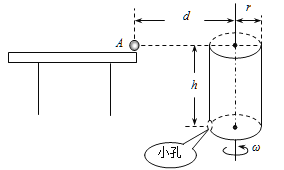
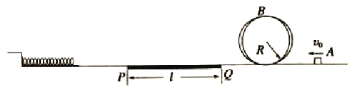
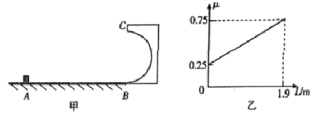
【题目】如图甲所示,半径![]() 的光滑半圆形轨道BC固定于竖直平面内,最低点B与水平面相切。水平面上有一质量为
的光滑半圆形轨道BC固定于竖直平面内,最低点B与水平面相切。水平面上有一质量为![]() 的物块从A点以某一初速度向右运动,并恰能通过圆弧轨道的最高点C,物块与水平面间的动摩擦因数为,且随离A点的距离L按图乙所示规律变化,A、B两点间距离
的物块从A点以某一初速度向右运动,并恰能通过圆弧轨道的最高点C,物块与水平面间的动摩擦因数为,且随离A点的距离L按图乙所示规律变化,A、B两点间距离![]() ,g取
,g取![]() 。求:
。求:
(1)物块经过最高点C时速度大小;
(2)物块经过圆弧轨道最低点B时对轨道压力的大小;
(3)物块在A点时的初速度。
【答案】(1)3m/s;(2)120N;(3)8m/s.
【解析】
(1)物块恰能通过圆弧轨道的最高点C,故由牛顿第二定律可得:mg=![]() ,
,
所以vC=![]() =3m/s;
=3m/s;
(2)物块在圆弧轨道上运动只有重力做功,故由机械能守恒可得:
![]() mvB2=
mvB2=![]() mvC2+2mgR=
mvC2+2mgR=![]() mgR,
mgR,
解得:![]() ;
;
再对物块在B点应用牛顿第二定律可得:FN=![]() +mg=6mg=120N;
+mg=6mg=120N;
那么由牛顿第三定律可得:物块经过圆弧轨道最低点时对轨道压力的大小为120N;
(3)物块在AB上运动只有摩擦力做功,摩擦力f=μmg=20μ(N),
故由图象可得:摩擦力做功Wf=20×![]() (0.25+0.75)×1.9J=19J;
(0.25+0.75)×1.9J=19J;
由动能定理可得:Wf=![]() mvB2
mvB2![]() mvA2,
mvA2,
解得:vA=8m/s

练习册系列答案
相关题目