题目内容
9. 如图所示,足够长的圆柱形气缸竖直放置,其横截面积为S=1×10-3m2,气缸内有质量m=2kg的活塞,活塞与气缸壁封闭良好,不计摩擦.开始时活塞被销子K销于如图位置,离缸底L1=12cm,此时气缸内被封闭气体的压强为P1=1.5×105 Pa,温度为T1=300K.外界大气压为P0=1.0×105Pa,g=10m/s2.
如图所示,足够长的圆柱形气缸竖直放置,其横截面积为S=1×10-3m2,气缸内有质量m=2kg的活塞,活塞与气缸壁封闭良好,不计摩擦.开始时活塞被销子K销于如图位置,离缸底L1=12cm,此时气缸内被封闭气体的压强为P1=1.5×105 Pa,温度为T1=300K.外界大气压为P0=1.0×105Pa,g=10m/s2.①现对密闭气体加热,当温度升到T2=400K,其压强P2多大?
②若在此时拔去销子K,活塞开始向上运动,当它最后静止在某一位置时,气缸内气体的温度降为T3=360K,则这时活塞离缸底的距离L3为多少?
③保持气体温度为360K不变,让气缸和活塞一起在竖直方向作匀变速直线运动,为使活塞能停留在离缸底L4=16cm处,则求气缸和活塞应作匀加速直线运动的加速度a大小及方向.
分析 ①由于销子的作用,气体的体积不会变化,确定气体的两个状态,分析其状态参量,利用等容变化可解得结果.
②拔去销子K后,活塞会向上移动直至内外压强一致,确定此时的状态参量,结合第一个状态,利用气体的状态方程可解的活塞距离缸底的距离.
③先根据理想气体状态方程列式求解封闭气体的气压,然后对活塞受力分析,求解加速度.
解答 解:①由题意可知气体体积不变,
状态Ⅰ:P1=1.5×105 Pa,T1=300K,V1=1×10-3×0.12m2
状态Ⅱ:P2=?T2=400K
气体发生等容变化,由查理定律得:
$\frac{{p}_{1}}{{T}_{1}}$=$\frac{{p}_{2}}{{T}_{2}}$,代入数据解得:P2=2×105pa;
②状态Ⅲ:p3=P0+$\frac{mg}{S}$=1.2×105pa,T3=360K,V3=1×10-3×lm2
由气体状态方程有:$\frac{{p}_{1}{V}_{1}}{{T}_{1}}$=$\frac{{p}_{2}{V}_{2}}{{T}_{2}}$,代入数据解得:l=0.18m=18cm;
③气体发生等温变化,由玻意耳定律得:p3L3S=p4L4S,代入数据解得:p4=1.35×105pa,
由牛顿第二定律得:p4S-p3S-mg=ma,代入数据解得:a=7.5m/s2,方向:竖直向上;
答:①现对密闭气体加热,当温度升到400K,其压强为2×105pa
②若在此时拔去销子K,活塞开始向上运动,当它最后静止在某一位置时,气缸内气体的温度为360K,则这时活塞离缸底的距离为18cm;
③气缸和活塞应作匀加速直线运动的加速度a大小为7.5m/s2,方向:竖直向上.
点评 该题考查了气体状态方程的应用,解答此类问题的关键就是正确的确定气体的状态,找出状态参量,利用相应的状态方程求解.在此过程中,正确的确定气体的压强是解题的关键.

 如图所示,小球从高处下落到竖直放置的轻弹簧上,从接触弹簧被压缩到最短的整个过程中,下列说法正确的是( )
如图所示,小球从高处下落到竖直放置的轻弹簧上,从接触弹簧被压缩到最短的整个过程中,下列说法正确的是( )| A. | 小球和弹簧的机械能守恒 | |
| B. | 在在最低点速度为零,加速度为零 | |
| C. | 速度一直在减小,直至速度为0,此时加速度最大 | |
| D. | 速度先增大再减小,直至为零 |

| A. | $\frac{{n}_{2}}{{n}_{1}}$<$\frac{{n}_{3}}{{n}_{4}}$ | |
| B. | $\frac{{n}_{2}}{{n}_{1}}$>$\frac{{n}_{3}}{{n}_{4}}$ | |
| C. | 升压变压器的输出电压等于降压变压器的输入电压 | |
| D. | 升压变压器的输出功率大于降压变压器的输入功率 |

| A. | 物体加速度相同 | B. | 物体克服摩擦力做功相同 | ||
| C. | 物体机械能增量相同 | D. | 恒力F1、F2对物体做功相同 |
| A. | 若使放射物质的温度升高,其半衰期可能变小 | |
| B. | Th核发生一次α衰变时,新核与原来的原子核相比,中子数减少了4 | |
| C. | 卢瑟福通过α粒子放射实验,提出了原子的核式结构模型 | |
| D. | 入射光的频率如果低于某金属的载止频率,即使增加该入射光的强度,也不能使该金属发生光电效应 | |
| E. | ${\;}_{92}^{218}$U经过一系列衰变后变为${\;}_{82}^{214}$Pb,则这个过程要经过8次α衰变,6次β衰变. |
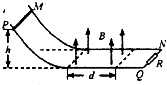 如图所示,MN和PQ是电阻不计的平行金属导轨,其间距为L,导轨弯曲部分光滑,平直部分粗糙,二者平滑连接.右端接一个阻值为R的定值电阻.平直部分导轨左边区域有宽度为d、方向竖直向上、磁感应强度大小为B的匀强磁场.质量为m、电阻也为R的金属棒从高度为h处静止释放,到达磁场右边界处恰好停止.已知金属棒与平直部分导轨间的动摩擦因数为μ,金属棒与导轨间接触良好.则金属棒穿过磁场区域的过程中( )
如图所示,MN和PQ是电阻不计的平行金属导轨,其间距为L,导轨弯曲部分光滑,平直部分粗糙,二者平滑连接.右端接一个阻值为R的定值电阻.平直部分导轨左边区域有宽度为d、方向竖直向上、磁感应强度大小为B的匀强磁场.质量为m、电阻也为R的金属棒从高度为h处静止释放,到达磁场右边界处恰好停止.已知金属棒与平直部分导轨间的动摩擦因数为μ,金属棒与导轨间接触良好.则金属棒穿过磁场区域的过程中( )| A. | 流过定值电阻的电流方向是N→Q | B. | 通过金属棒的电荷量为$\frac{BdL}{2R}$ | ||
| C. | 金属棒滑过$\frac{d}{2}$时的速度大于$\frac{\sqrt{2gh}}{2}$ | D. | 金属棒产生的焦耳热为$\frac{1}{2}$(mgh-μmgd) |
 如图,△OAC的三个顶点的坐标分别为O(0,0)、A(0,L)、C($\sqrt{3}$L,0),在△OAC区域内有垂直于xOy平面向里的匀强磁场.在t=0时刻,同时从三角形的OA边各处以沿y轴正向的相同速度将质量均为m,电荷量均为q的带正电粒子射入磁场,已知在t=t0时刻从OC边射出磁场的粒子的速度方向垂直于y轴.不计粒子重力和空气阻力及粒子间相互作用.
如图,△OAC的三个顶点的坐标分别为O(0,0)、A(0,L)、C($\sqrt{3}$L,0),在△OAC区域内有垂直于xOy平面向里的匀强磁场.在t=0时刻,同时从三角形的OA边各处以沿y轴正向的相同速度将质量均为m,电荷量均为q的带正电粒子射入磁场,已知在t=t0时刻从OC边射出磁场的粒子的速度方向垂直于y轴.不计粒子重力和空气阻力及粒子间相互作用.
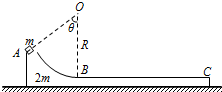 如图所示,静止在光滑水平面上的弧形木板质量为2m,AB部分是半径为R=0.6m、圆心角θ=60°的光滑圆弧轨道,BC部分是长为L=0.75m的粗糙水平轨道.一质量为m的小物块(视为质点)从A处轻轻释放后恰好滑到达C点.重力加速度取g=10m/s2.求:
如图所示,静止在光滑水平面上的弧形木板质量为2m,AB部分是半径为R=0.6m、圆心角θ=60°的光滑圆弧轨道,BC部分是长为L=0.75m的粗糙水平轨道.一质量为m的小物块(视为质点)从A处轻轻释放后恰好滑到达C点.重力加速度取g=10m/s2.求: